Olá leitores!
Hoje trazemos mais uma dúvida de uma de nossas leitoras. Esta dúvida envolve o conceito de máximo e mínimo envolvendo o trinômio do segundo grau. Vamos lá:
Um restaurante a quilo vende  quilos de comida por dia, a
quilos de comida por dia, a 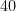 reais o quilo. Uma pesquisa de opinião revelou que, cada aumento de um real no preço do quilo, o restaurante perde oito clientes por dia, com um consumo médio de
reais o quilo. Uma pesquisa de opinião revelou que, cada aumento de um real no preço do quilo, o restaurante perde oito clientes por dia, com um consumo médio de  gramas cada. Qual deve ser o valor do quilo de comida, em reais, para que o restaurante tenha a maior receita possível por dia?
gramas cada. Qual deve ser o valor do quilo de comida, em reais, para que o restaurante tenha a maior receita possível por dia?
a) 
b) 
c) 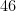
d) 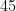
e) 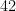
Enviado por Laura Helena
Bom, vamos lá. Para saber quanto o restaurante ganha por dia com a venda de refeições, sabemos que o total, em reais, será o quantos quilos de comida são vendidas por dia para cada cliente multiplicado pelo preço do quilo e pelo número total de clientes. Por exemplo, se são vendidos  quilo a
quilo a 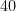 reais para cada quilo e são
reais para cada quilo e são 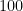 clientes no dia, teremos um total de
clientes no dia, teremos um total de  reais por dia.
reais por dia.
Daí, vamos nomear as variáveis. Chamaremos de 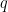 o total de quilos vendidos por dia no restaurante; de
o total de quilos vendidos por dia no restaurante; de  o preço do quilo neste restaurante;
o preço do quilo neste restaurante;  vai ser o número de reais aumentados no preço do quilo.
vai ser o número de reais aumentados no preço do quilo.
Antes de escrever a função que calcula o total, precisamos saber quanto cada cliente consome em média. No enunciado, é dito que cada cliente consome  g (no caso
g (no caso  kg) e são vendidos
kg) e são vendidos 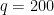 quilos por dia. Ou seja,
quilos por dia. Ou seja, 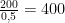 clientes por dia.
clientes por dia.
Do enunciado também sabemos que a cada aumento de um real no preço teremos oito clientes a menos. Assim, ao aumentar  reais, no preço, tornando-o
reais, no preço, tornando-o 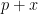 , diminuiremos
, diminuiremos 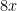 clientes no total. Veja: se aumentamos
clientes no total. Veja: se aumentamos  reais, perdemos
reais, perdemos 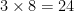 clientes. Agora sim, vamos lá.
clientes. Agora sim, vamos lá.
A arrecadação (receita) do restaurante  é dada por:
é dada por:
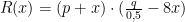
Substituindo os valores de  e
e 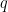 :
:
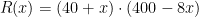
Vamos testar esta expressão. Se  , teremos
, teremos 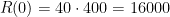 reais. Mas ao aumentar, por exemplo, um real
reais. Mas ao aumentar, por exemplo, um real  , teremos um preço de
, teremos um preço de  reais, porém
reais, porém  clientes. Na função, teríamos:
clientes. Na função, teríamos:
 reais
reais
Agora vamos desenvolver a função:
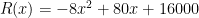
A receita máxima ocorre para 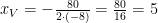 . Como o preço inicial era de
. Como o preço inicial era de 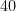 reais, sabemos que o preço para o qual a receita é máxima é o de
reais, sabemos que o preço para o qual a receita é máxima é o de 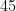 reais. Opção D.
reais. Opção D.
Veja que a variação é pequena e dava pra “chutar” olhando as opções.
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
https://apoia.se/mentor
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]
no desenvolvimento
.
. Assim, nosso termo geral será da forma:
, teremos
, finalmente
, logo
. Assim, o termo procurado é o quinto termo. Teremos:
. Assim, o termo procurado é
.











