Na última terça-feira, dia 7/4/2026, rolou uma revisão de vários assuntos aqui no Colégio Mentoria, preparando os alunos para a prova de matemática da próxima semana que corresponderá a AV2.
Boa parte das questões da revisão foram resolvidas em sala e a playlist relacionada está no link abaixo:
Além disso, vamos disponibilizar também a lista de exercícios relacionada a essa playlist acima, você pode baixá-la clicando em:
Mas não é só isso! Na próxima sexta-feira, dia 10/4/2026, vai rolar mais uma revisão. Desta vez de álgebra. E, em breve, deixaremos também a playlist relacionada logo a seguir. Mas, por enquanto, deixamos somente a lista de exercícios abaixo:
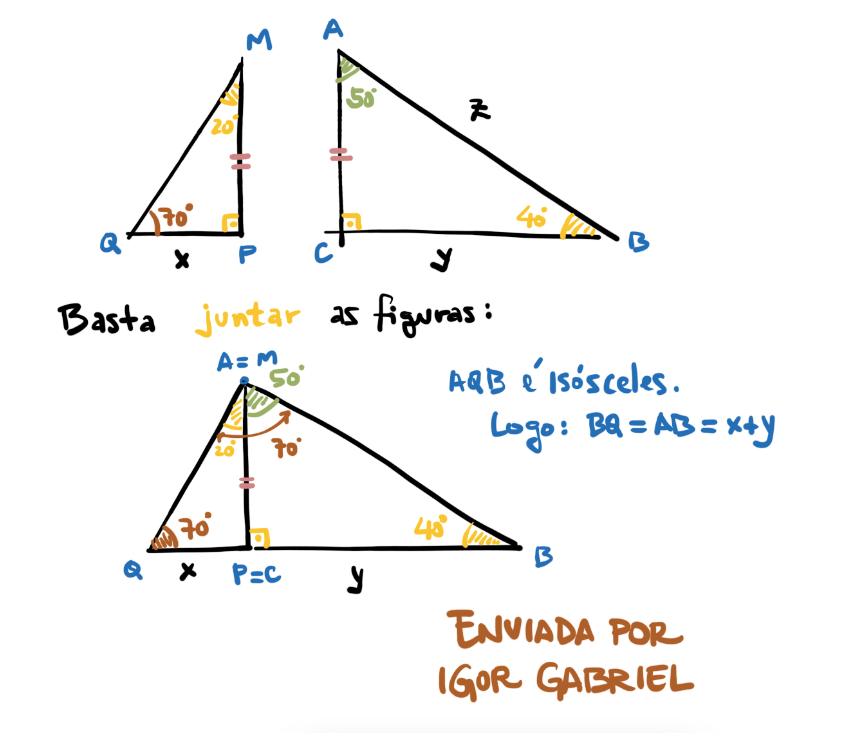
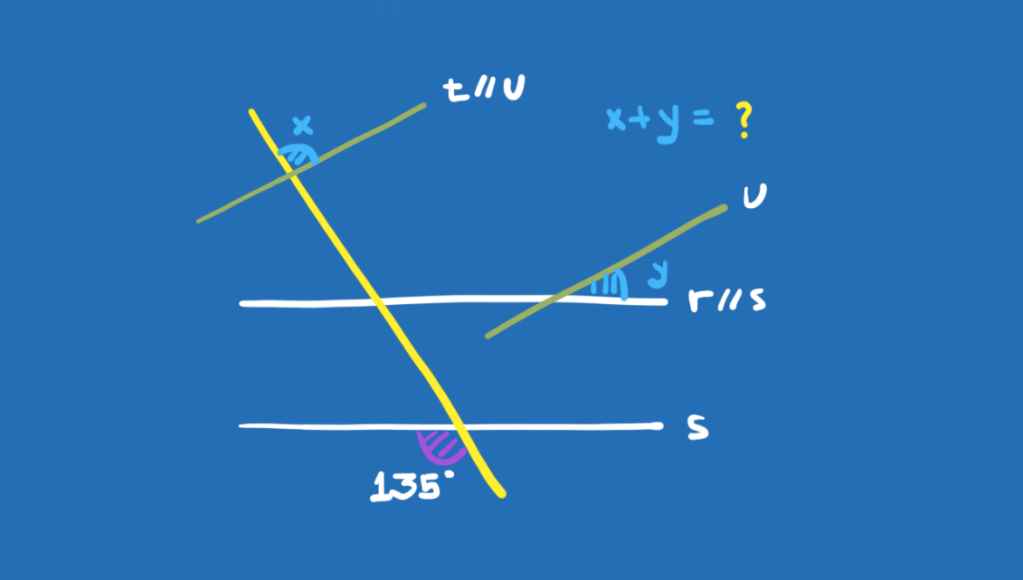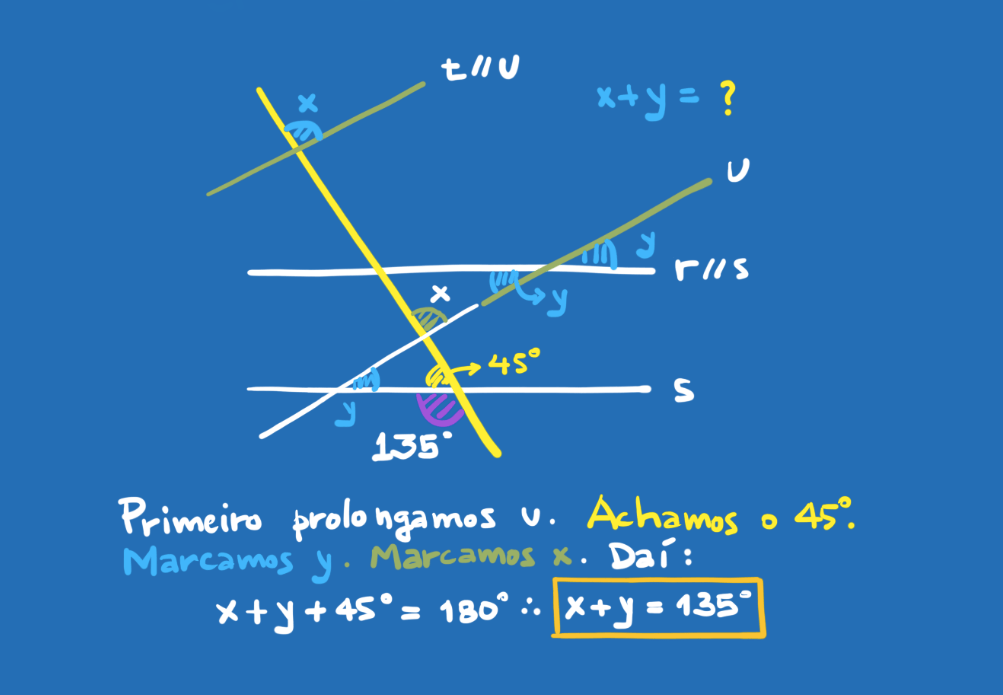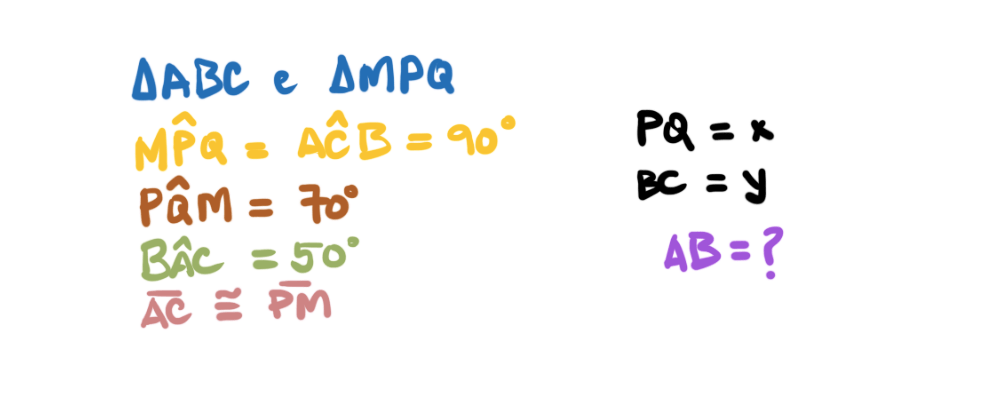No último sábado, dia 10 de janeiro de 2026, foram realizadas mais duas edições da nossa prova de bolsas em ambas as unidades do Colégio Mentoria (Natal e Parnamirim).
Este é um momento muito importante para que pais/responsáveis entendam e conheçam, não só a infraestutura oferecida pela escola, mas também a proposta educacional.
Os alunos que compareceram ao evento pleiteavam um desconto para as turmas de colégio (do 6º ano do ensino fundamental à 3ª série do ensino médio) e, desta vez, também para as turmas de cursos preparatórios, podendo chegar a bolsas de até 100% de desconto nas parcelas da anuidade.
Se você perdeu essa oportunidade, não se desespere! Pois ainda e possível se matricular com um preço bastante acessível.
Em entrevista ao Blog do Mentoria, ainda durante a prova, Diego Gorito (gestor da escola) comentou: “Nossos atendentes estão sempre autorizados a fechar um bom negócio para cada um que nos procura.” Ele continuou ainda reforçando a meta da instituição: “Queremos apenas oferecer educação de qualidade…” completa.
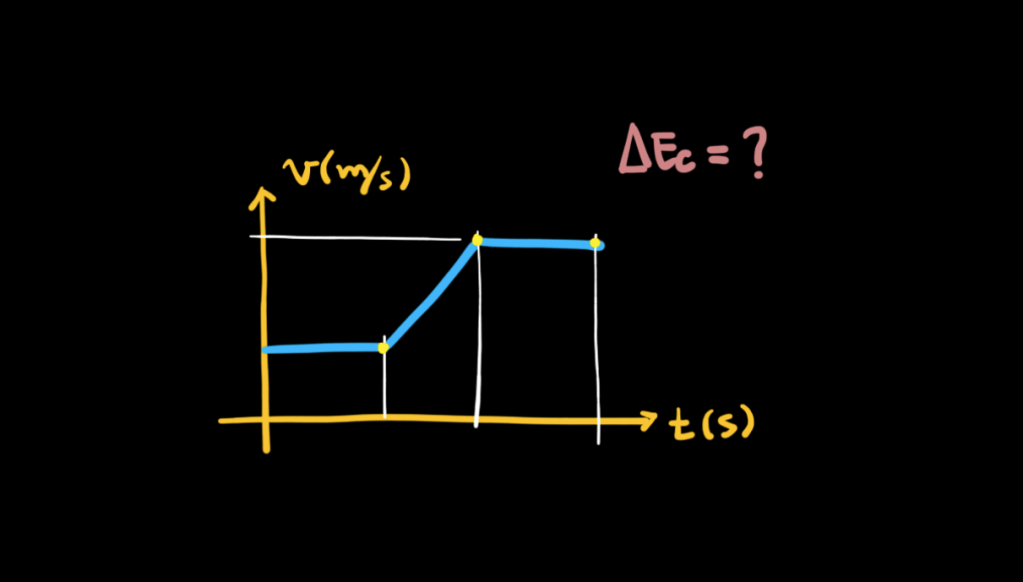
As provas foram compostas de 10 questões de matemática e 10 questões de língua portuguesa para as turmas de 6º e 7º ano, como sempre. Para as demais turmas, houve mais 10 questões de língua inglesa. O resultado sai praticamente na hora, e o responsável já pode aproveitar a oferta. “É o que muitos pais fazem, já resolvem tudo de uma vez.” Diz Diego.
As provas são simples. Em geral as questões abordam conteúdos dos anos iniciais e são divididas por nível de dificuldade, sendo 50% fáceis, 30% médias e 20% difíceis.
“A coordenação procura bons alunos e, ao longo de todas as provas de bolsas aplicadas, vimos que este é um modelo que atende bem o que procuramos.” Disse Juliana Gorito, uma das gestoras educacionais do Mentoria.
Os pais compareceram em peso. Para eles, enquanto os candidatos fazem a prova, é feita uma reunião explicando a metodologia da escola para que saibam como tudo funciona e possam esclarecer todas as dúvidas.
A dica que Diego e Juliana dão aos pais e responsáveis é: “As vagas são limitadas e devemos procurar o quanto antes, pois todo mundo quer uma escola que trabalhe em cima da disciplina. E isso é o que fazemos!”
Como sempre há aqueles que deixam para a última hora, eles trazem um convite: “Haverá mais oportunidades, fiquem ligados em nossas redes sociais.”
É galera, o ano de 2025 está acabando…, mas calma, não sem antes trazer inúmeras memórias incríveis para todos nós. No último sábado, dia 25 de outubro de 2025, ocorreu o derradeiro aulão da série de aulões para o IFRN ocorridos no Colégio Mentoria e que já fazem parte de nossa cultura desde 2023.
O Evento em Si
Este evento foi entitulado Aulão V4 em referência a célebre frase: “Vim, vi, venci.” de Julio Cesar, parafraseando e acrescentando apenas a palavra “Véspera”. Isto ocorre por que a referida aula aconteceu, como de costume, na véspera da prova do IFRN de 2025. Portanto, contemplando assim os 4 V’s que aparecem no citado título.
Em termos de números, foi um dos maiores (ou até mesmo o maior dos) aulões já organizados por nós, contando com duas salas de aulas completamente lotadas, tendo aulas simultaneamente de forma alternada de língua portuguesa (incluindo redação) e matemática voltadas exclusivamente para uma revisão final muito especial de conteúdo focadas em dicas, atalhos e lembretes muito importantes do que mais tem sido abordado neste concurso ao longo dos últimos anos.
Compareceram ao evento cerca de 80 alunos de ambas as unidades e 50% das vagas disponibilizadas foram vendidas em incríveis menos de 24 h da abertura das inscrições. Isto revela e até mesmo ressalta a grandeza e a importância que o evento tem para os alunos, dado que trata-se da véspera de uma prova tão significativa. E detalhe: para muitos desses alunos este será o primeiro concurso real de sua vida estudantil.
Um Pouco da Nossa História
Começamos a trabalhar com o público do IFRN em 2023 e “de lá para cá” já aprovamos mais de 150 alunos e, somente no ano de 2024, aprovamos mais de 80 alunos e conseguimos emplacar 10 primeiros lugares em cursos diversos, além de 7 segundos lugares.
Considerando que a nossa tradição está apoiada nos concursos militares, este é um feito notável e que, com certeza, é fruto de nossa dedicação e claro, da adaptação de um método continuado de estudo que vem sendo aplicado em concursos para escolas militares.
É verdade que muitos alunos sentem a grande mudança no começo porque a rotina de estudo é pesada e com vários simulados ao longo do ano. Em 2025, ultrapassamos 20 simulados entre presenciais e online, sendo que os presenciais foram mais de 70% desta quantidade.
Então, finalmente, a “missão” foi cumprida. Infelizmente é momento de despedida dos alunos, pois é uma certa rotina que está se encerrando; mas isto claramente faz parte de um ciclo.
Sabemos que é assim. E repetiremos a rotina de dedicação e bons hábitos ano que vem. Aos que vão, um até logo; aos que ainda virão, sejam muito bem vindos. O sucesso espera por vocês!
Segue uma pequena lista de exercícios sobre o início da trigonometria envolvendo a parte inicial de círculo trigonométrico, arcos côngruos e arcos notáveis. Além disso, há alguns exercícios simples de trigonometria no triângulo retângulo. Segue a lista:
Com um pequeno atraso por questões alheias, publico o problema desta semana. Este exercício já é bem antigo, mas vale a pena conhecer, tanto pelo formato quanto pela ideia que ele traduz de o quão as equações são muito poderosas em resolver problemas elementares. Segue o enunciado:
Tenho o dobro da idade que você tinha quando eu tinha a idade que você tem. Quando você tiver minha idade, nossas idades somarão . Quais serão nossas idades daqui a anos?
Vale a pena a tentativa! Mãos a obra e bora pra cima!
e 
s. A massa vale 
kg. Então:
. A solução segue abaixo:
. Quais serão nossas idades daqui a 
Blog do Mentoria 