Segue mais uma dúvida de nossos alunos:
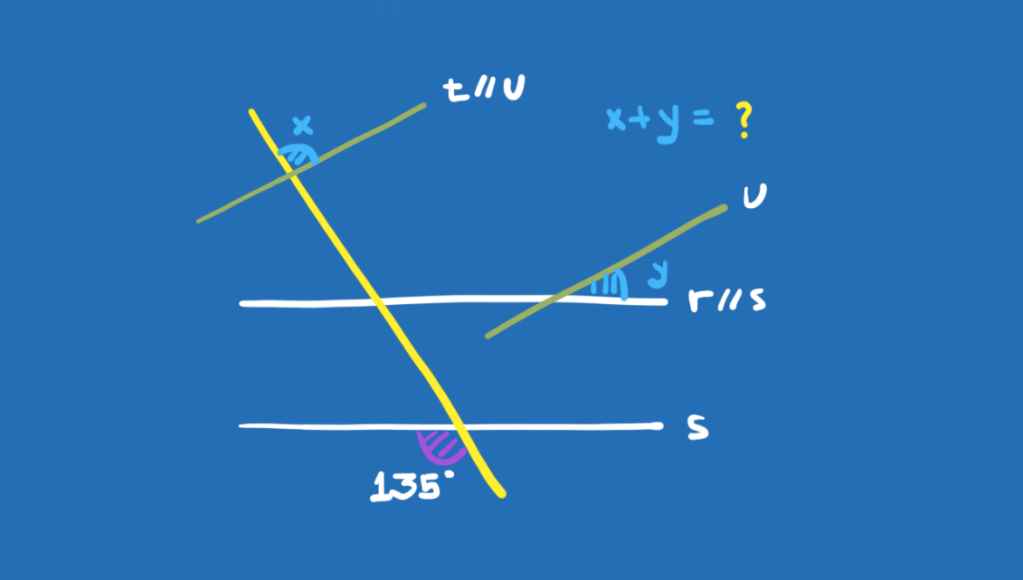
Cuja solução segue abaixo:
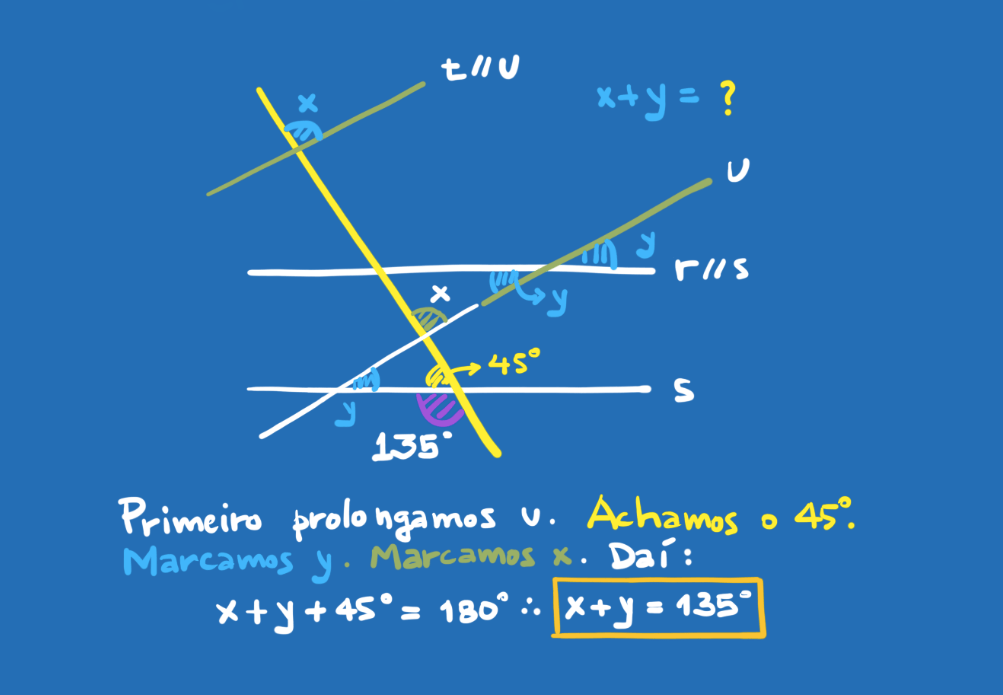
Nossa loja de camisetas: http://reserva.ink/equilateral
Segue mais uma dúvida de nossos alunos:
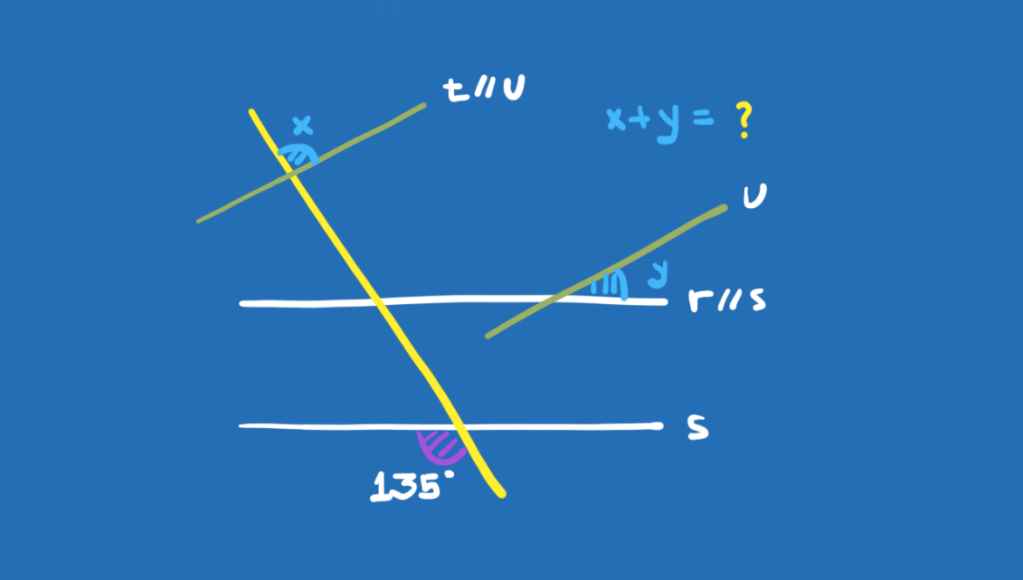
Cuja solução segue abaixo:
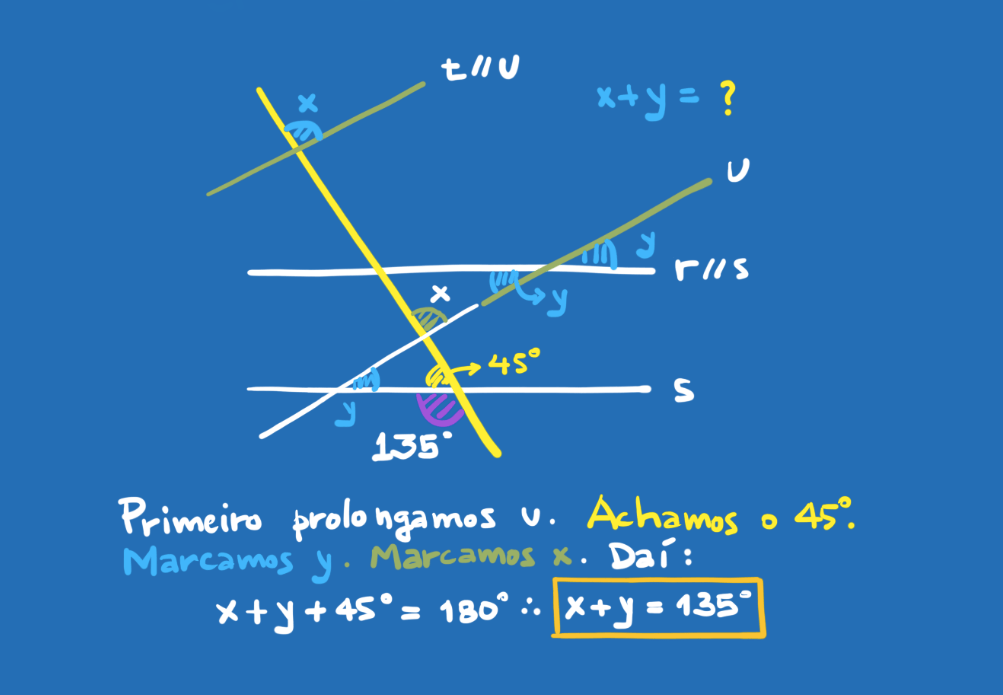
Nossa loja de camisetas: http://reserva.ink/equilateral
Olá, hoje trago um problema proposto como dúvida por uma aluna. O problema envolve apenas o conceito de ponto médio de segmentos e as medidas de alguns segmentos adjacentes. O enunciado não traz a figura e, por isso, desenhar uma boa figura já ajuda em boa parte para resolver o problema.
Segue o enunciado abaixo.
Antes de ver a solução, tente resolver sozinho. O conceito de segmento de reta é simples e faz parte do início do estudo da geometria plana. É importante para formular e resolver problemas e ajuda em várias áreas como, por exemplo, trigonometria e/ou geometria analítica.
Se você já tentou resolver e não conseguiu, segue abaixo a solução. Mas é importante tentar, lembre-se que a dúvida é o start importante para a construção do conhecimento.
E aí, acertou?
Mande seus comentários para nós!
[LSB]
Segue a dúvida de um de nossos alunos a respeito de sistemas de bases de numeração. O assunto costuma ser cobrado no Colégio Naval e na EPCAr além de outras provas (concursos) e, justamente por isso, vamos comentar a solução deste problema aqui. Eis a pergunta:
O número
corresponde na base
a:
a)
b)
c)
d)
e)
Como sabemos, para passar da base para a base
só precisamos “expandir” o número na base dada e realizar os cálculos na base
. Então, para o número dado, teríamos:
Veja que a parte decimal começa a ter os expoentes inteiros negativos, seguindo a partir do zero que é o expoente da base correspondente à ordem das unidades. Então, desenvolvendo:
Como , teremos
, ou seja, opção C.
Entendeu? Então tente converter, por exemplo, para a base
e me conte o que encontrou nos comentários abaixo.
Um grande abraço e nos vemos por aí.
[LSB]
Olá leitor.
Hoje trazemos um problema que envolve um sistema de equações não lineares e que, a princípio, parece fácil, mas na realidade, envolve métodos mais sofisticados que simplesmente substituir uma equação na outra. Veja o problema a seguir:
Sejam
,
e
números complexos que satisfazem o sistema de equações abaixo:
O valor da soma
é:
a)
b)
c)
d)
e)
Enviada por Matheus
Podemos inicialmente pensar em um polinômio tal que
,
e
sejam exatamente suas raízes e seja escrito como:
Das relações de Girard e do sistema dado chegamos a:
Alem disso, sabendo que , portanto:
Da última equação do sistema:
Ou seja . Finalmente, podemos usar as somas de Newton:
Teremos:
Como , temos:
Chegando à opção B.
Como observação, não nos estendemos sobre as somas de Newton, mas o faremos em momento oportuno!!!
Até a próxima!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]
Olá leitor!
Segue uma questão sobre análise combinatória trazida até mim.
(ITA) Uma escola possui
professores, sendo
de Matemática,
de Física e
de Química. De quantas maneiras podemos formar comissões de
professores de modo que cada uma contenha exatamente
professores de Matemática, no mínimo
de Física e no máximo
de Química?
a)
b)
c)
d)
e) N.D.A.
Enviada por Caio Franco
Esse é o tipo de problema que a boa e velha tática de separar em casos ajuda bastante. Vamos montar uma tabela com as possibilidades de números de professores, sendo para Matemática;
para Física;
para Química e
para as outras disciplinas.
Assim, o total de escolhas será:
Podemos colocar em evidência:
Opção D.
Uma questão não tão difícil, mas no padrão que se espera do ITA.
Até a próxima!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]
Olá, leitores!
estamos de volta. Desta vez, vamos resolver dois problemas envolvendo números binomiais. Só pra lembrar, um número binomial é definido como , com
e
em que o símbolo
é o fatorial do número
. Vamos lá:
Calcular:
Enviado por Stephanie Wenceslau
Desenvolvendo, de acordo com a definição:
Daí:
Simplificando:
Continuando:
Finalmente teremos . As raízes são
e
. Como
teremos
.
Calcular:
Enviado por Stephanie Wenceslau
Vamos lá, desenvolvendo:
Teremos:
Cancelando os devidos termos:
Veja que, por mera observação, ja que temos
.
E aí? O que achou?
Até a próxima!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]
Dúvida enviada por Priscila.
(CETF-RJ/2007/Q11) Ao dividirmos o termo de ordem de uma P.A. pelo termo de ordem
, obteremos
por resposta. Ao se dividir o décimo termo dessa seqüência pelo terceiro termo, obteremos o quociente
e o resto
. A soma dos termos da P.G. cuja razão e o primeiro termo são os mesmos da P.A. é:
Solução: Do enunciado sabemos que e que
.
Mas sabemos que e que
, então:
Com isso chegamos a .
Além disso, e
. Voltando ao enunciado podemos escrever:
Substituindo o encontrado:
Então . E, deste modo,
. Como a soma
dos termos de uma P.G. com razão
tal que
é
, podemos fazer:
Espero ter ajudado.
Questão enviada por Sebastião Soares:
Se e
, então
é igual a:
a)
b)
c)
d)
e)
Você pode ver a solução comentada aqui.