Olá leitores.
Recebi estes dias uma dúvida que envolve o fatorial de um número e sua divisibilidade por 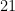 . Vamos ver o enunciado e resolver:
. Vamos ver o enunciado e resolver:
(EN) O fatorial de  é divisível por
é divisível por  . O maior valor inteiro de
. O maior valor inteiro de  é:
é:
a) 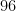
b) 
c) 
d) 
e) 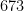
Marcus Tavares
Bom, vamos ao que interessa. Para que um número seja divisível por 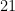 é necessário que ele seja divisível por
é necessário que ele seja divisível por  e por
e por 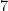 . Então vejamos o seguinte:
. Então vejamos o seguinte:  só é divisível por
só é divisível por 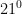 e
e  , pois:
, pois:

Assim, fica claro que calculando 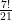 teremos um inteiro, pois temos um fator de
teremos um inteiro, pois temos um fator de 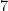 e, pelo menos, um fator de
e, pelo menos, um fator de  em
em  . Se continuarmos investigando os fatoriais consecutivos e maiores que
. Se continuarmos investigando os fatoriais consecutivos e maiores que  , isto não ocorrerá novamente até o
, isto não ocorrerá novamente até o 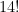 , veja:
, veja:

Fica explícito que 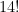 é divisível por
é divisível por 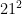 , mas não por
, mas não por  , pois há apenas dois fatores de
, pois há apenas dois fatores de 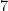 , sendo um no próprio
, sendo um no próprio 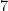 e o outro no
e o outro no 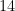 , embora haja muito mais fatores de
, embora haja muito mais fatores de  .
.
Esse processo continua da mesma maneira até chegarmos ao 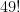 , pois
, pois  , acrescentando, por sua vez, dois fatores de
, acrescentando, por sua vez, dois fatores de 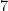 . Chegamos, a partir daí a seguinte conclusão:
. Chegamos, a partir daí a seguinte conclusão:
- cada múltiplo de
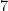 acrescenta um fator de
acrescenta um fator de 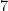 ;
; - cada múltiplo de
 acrescentará dois fatores de
acrescentará dois fatores de 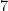 , dos quais um já foi contado nos fatores de
, dos quais um já foi contado nos fatores de 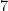 ;
; - cada fator de
 acrescentará três fatores de
acrescentará três fatores de 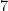 , dos quais dois já foram contados: um deles nos múltiplos de
, dos quais dois já foram contados: um deles nos múltiplos de 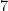 e o outro nos múltiplo de
e o outro nos múltiplo de 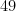 ;
;
Então vamos lá! Vamos calcular quantos múltiplos de  há de
há de 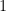 a
a  :
:
- Sabemos que
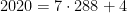 , logo há
, logo há  múltiplos de
múltiplos de 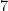 de
de 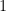 a
a  ;
; - Continuando, temos
 , portanto, há
, portanto, há  múltiplos de
múltiplos de 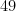 no mesmo intervalo; e
no mesmo intervalo; e - Finalmente,
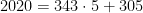 , havendo, então,
, havendo, então,  múltiplos.
múltiplos. - Não há múltiplos de
 , pois
, pois  .
.
Contando agora teremos:
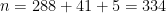 fatores de
fatores de 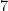 em
em 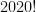
Veja que, se a pergunta fosse, “quantos são os possíveis valores inteiros de  “, ainda incluiríamos o zero, ficando com
“, ainda incluiríamos o zero, ficando com  valores possíveis, sendo o
valores possíveis, sendo o  o maior deles!
o maior deles!
Espero ter esclarecido!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
https://apoia.se/mentor
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]










