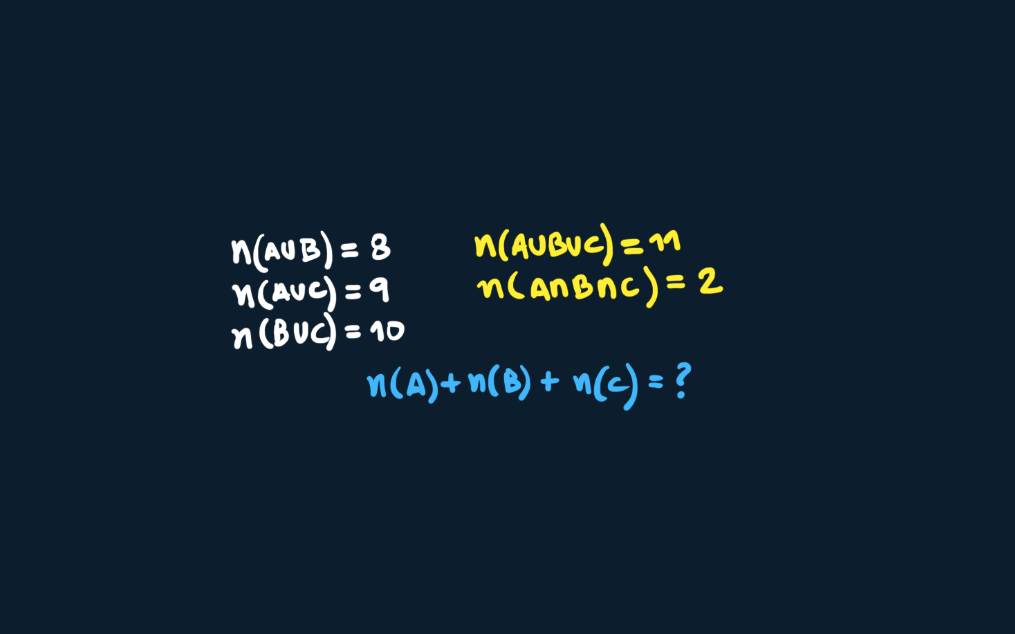Tira-Teima #2

LIVE: Aplicação de Conjuntos

Sejam bem vindos a mais uma LIVE. Vou deixar aqui todo o material utilizado na LIVE de ontem. Mas antes, já vai se ligando nos principais links:

Para entrar no grupo do WhatsApp e receber gratuitamente as listas toda semana: CLICA AQUI AGORA MESMO!
Para ver nosso instagram: CLICA AQUI PARA IR LÁ!
Receba ebooks gratuitos: CLICA AQUI E RECEBA TEUS EBOOKS!
Ajude o site comprando meu e-book de Física para a EEAR: O MELHOR LIVRO PARA A EEAr ESTÁ AQUI!

Agora vamos aos arquivos de ontem:

O “quadro” de ontem:

Você pode pegar a lista de exercícios clicando AQUI.

É isso, até a próxima!

Eu sou Leonardo e você veio ao lugar certo pra aprender!

Está é uma iniciativa para trazer materiais de boa qualidade até você e te ajudar a aprender mais.

Vamos crescer mais! Faça parte:

— Doe via PIX: leonardosantos.inf@gmail.com

— Siga-nos nas redes:

Instagram: http://www.instagram.com/mentorblog_oficial

Facebook: https://www.facebook.com/cursomentor

— DIVULGUE esta iniciativa!

Até a próxima!

[LSB]

Live: Introdução aos Conjuntos

Para quem quiser a lista de exercícios resolvida nesta live, entre em nosso grupo de WhatsApp indo AQUI.

O “quadro” com as imagens das questões e suas resoluções está aqui:

Minha iniciativa é GRATUITA.

AJUDE:

👉🏼 Doe qualquer quantia via PIX: leonardosantos.inf@gmail.com

👉🏼 Siga-nos:

http://www.instagram.com/mentorblog_oficial

E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800:

👉🏼 DIVULGUE esta iniciativa!

Até!

[LSB]

Conjuntos, Múltiplos e Primos na Escola Naval

Olá leitor,

trazemos uma questão da prova de 2019/2020 da Escola Naval com um enunciado nem tão bem escrito assim, mas que tem uma abordagem interessante sobre a teoria de conjuntos. Vamos lá:

(Escola Naval) Seja $W$ o conjunto dos números múltiplos de $2$ ou $P$ , em que $P$ é um primo ímpar. Sabendo que $\frac{3}{5}$ de $W$ , que são múltiplos de $P$ , são ímpares; $\frac{2}{5}$ de $W$ são ímpares; e $77$ elementos de $W$ não são múltiplos de $2P$ , pode-se afirmar que a quantidade de elementos de $W$ que são ímpares é um número múltiplo de:
a) $4$
b) $5$
c) $7$
d) $9$
e) $11$
Enviado por Marcus Tavares

Bom, em primeiro lugar, o enunciado já traz uma inadequação (pra não dizer equívoco) no início, uma vez que os múltiplos de $2$ ou $P$ são infinitos. Assim, deveria vir escrito que $W$ é conjunto finito. Mas deixando isto de lado considere a figura a seguir:

Vamos considerar que $M_P$ é o conjunto dos múltiplos de $P$ e que $M_2$ é o conjunto dos múltiplos de $2$ .

Vamos considerar que $M_P$ é o conjunto dos múltiplos de $P$ e que $M_2$ é o conjunto dos múltiplos de $2$ .

Desse modo:

$a$ serão os múltiplos de $2$ que não são múltiplos de $P$ ;
$b$ serão os múltiplos de $2$ que também são múltiplos de $P$ , ou seja, como $P$ também é primo, serão os múltiplos de $2P$ ; e
$c$ serão os múltiplos de $P$ que não são múltiplos de $2$ ; portanto, correspondem aos múltiplos ímpares de $P$ .

Chamando o total de elementos de $x$ , do enunciado, tiramos as seguintes informações:

$\left\{ \begin{array}{l} a+b+c = x \\ c = \frac{2}{5} x \\ c + a = 77 \\ \frac{3}{5}(c + b) = c \\ \end{array} \right.$

Um comentário meu: com relação à última linha do sistema anterior, acho que o enunciado foi muito mal escrito, bastava dizer “dos múltiplos de $P$ , $\frac{3}{5}$ são ímpares”. Mas enfim, teremos, da última linha:

$3c + 3b = 5c \Rightarrow b = \frac{2}{3} c$

Da segunda linha, escrevemos: $b = \frac{2}{3} \cdot \frac{2}{5} \cdot x = \frac{4}{15} x$ e da terceira linha:

$\frac{2}{5} x + a = 77 \Rightarrow a = 77 - \frac{2}{5} x$

Agora, todas as variáveis estão em função de $x$ , voltando à primeira linha do sistema:

$a + b + c = x \Rightarrow 77 - \frac{2}{5} x + \frac{4}{15} x + \frac{2}{5} x = x$

Então:

$\frac{11}{15} x = 77 \Rightarrow x = 105$

Como queremos apenas os valores ímpares, poderíamos simplesmente dizer: “infinitos”, mas lembre-se que o enunciado foi mal escrito (ou de má vontade ou ambos) e queremos o valor de $c$ neste caso. Assim $c = \frac{2}{5} \cdot 105 = 42$ que é múltiplo de $7$ . Opção C.

Até mais!

Anúncios

Minha iniciativa é GRATUITA.

Você pode AJUDAR:

— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com

— Pelo APOIA SE:

https://apoia.se/mentor

— Nos seguindo:

http://www.instagram.com/curso_mentor_oficial

Mas, claro, fique a vontade, qualquer ajuda é bem vinda!

E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!

Entre em nosso canal no Telegram: https://t.me/cursomentor

Apoiadores:

Edson Pereira Barros

Até!

[LSB]

Probabilidade e M.D.C na Escola Naval

Olá leitor,

a prova da Escola Naval de 2020/2021 trouxe uma questão que envolve o M.D.C de dois números e uma pergunta sobre probabilidade. Segue a questão:

(EN) Escolhendo aleatoriamente um número do conjunto $\{1;2;3;\ldots;2020\}$ , qual a probabilidade de que o número escolhido e $2020$ sejam primos entre si?
a) $\frac{40}{101}$
b) $\frac{153}{1010}$
c) $\frac{293}{1010}$
d) $\frac{401}{1010}$
e) $\frac{76}{505}$
Enviada por Stephanie Wenceslau

Bom, primeiro, precisamos saber o que são números primos entre si ou ainda mutuamente primos. Dizemos que dois números naturais $a$ e $b$ são primos entre si, se $\textrm{mdc} (a,b) = 1$ . O m.d.c. entre dois números naturais vale $1$ se eles não possuem fatores comuns em sua fatoração em primos. Por exemplo, $9$ e $16$ são primos entre si, pois veja que $9 = 3^2$ e $16 = 2^4$ .

É possível ver que dois números pares nunca são primos entre si, pois ambos são divisíveis por $2$ ; e, que dois números primos também sempre são primos entre si, por conta da própria definição de números naturais primos.

Assim, fatorando $2020$ , encontramos $2020 = 2^2 \cdot 5 \cdot 101$ . Ou seja, todos os múltiplos de $2$ , $5$ ou $101$ não serão primos com $2020$ , pois haverá fatores comuns em suas fatorações, tornando o m.d.c entre eles maior que $1$ .

Vamos contar então, primeiramente, os múltiplos de $2$ . Eles são em número $M(2) = 1010$ . Para $5$ , temos $M(5) = 404$ . Finalmente, para $101$ , ficamos com $M(101) = 20$ .

Agora, ao somarmos estes valores, teremos $M(2) + M(5) + M(101) = 1010 + 404 + 20 = 1434$ . Porém, precisamos atentar para o fato de que, estamos contando números repetidos, uma vez que os múltiplos de $10$ , por exemplo, são múltiplos de $2$ e de $5$ também; sendo, portanto, recontados. Vamos excluí-los.

Os múltiplos de $2$ e de $5$ são os múltiplos de $10$ , e são $M(10) = 202$ . Para os múltiplos de $2$ e de $101$ , teremos $M(202) = 10$ ; e, finalmente, os múltiplos de $5$ e de $101$ são em número total de $M(505) = 4$ . Estes serão excluídos. O total é $M(10) + M(202) + M(505) = 202 + 10 + 4 = 216$ .

Ainda precisamos considerar os múltiplos simultâneos de $2$ , $5$ e $101$ , que serão os múltiplos de $1010$ . Estes são excluídos mais de uma vez e precisam ser reincluídos. Então $M(1010) = 2$ .

Finalmente podemos encontrar todos os números naturais que têm fatores comuns com $2020$ , não sendo primos com $2020$ . Assim, eles são $1434 - 216 + 2 = 1220$ no total. Como são $2020$ números no total, temos $2020 - 1220 = 800$ números que são primos entre si com $2020$ . Agora, temos a probabilidade:

$P = \frac{800}{2020} = \frac{40}{101}$

Opção A.

E aí, gostou.

Siga-me e ajude divulgando.

Anúncios

Minha iniciativa é GRATUITA.

Você pode AJUDAR:

— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com

— Pelo APOIA SE:

https://apoia.se/mentor

— Nos seguindo:

http://www.instagram.com/curso_mentor_oficial

Mas, claro, fique a vontade, qualquer ajuda é bem vinda!

E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!

Entre em nosso canal no Telegram: https://t.me/cursomentor

Apoiadores:

Edson Pereira Barros

Até!

[LSB]

Uma Dúvida Interessante Sobre Conjunto-Solução

Olá pessoal, há algum tempo, recebi este comentário aqui no site. Como um dos vídeos mais vistos em nosso canal no Youtube (veja ele aqui ou no final desta postagem!) trata deste assunto, resolvi resolver e comentar um pouco sobre isto.

A dúvida é da Helena e diz o seguinte:

Se a equação $X^4 - KX^2 = 0$ tem solução $S = \{-9;0;9\}$ , então:
a) $K=9$
b) $K=81$
c) $K=18$
d) $K=0$
e) $K= -9$
Helena

Inicialmente quero agradecer pela interação com o site, que por muito tempo ficou parado e que agora minha meta é manter funcionando. Bom, vamos lá. Em primeiro lugar, vamos considerar algumas coisas.

(1) Vamos adotar que a equação tem $X$ como incógnita, ou seja, este é o valor que queremos calcular. Isto faz sentido, porque se $K$ fosse a variável, bastaria isolar $K$ , fazendo:

$-KX^2 = -X^4 \Rightarrow K = {X^2} \qquad \textrm{para } X \ne 0$

Mas, como esta é uma equação literal do primeiro grau na incógnita $K$ , seu conjunto-solução só poderia admitir um único valor. O que contrariaria o enunciado.

(2) O que o enunciado chama de “solução” na realidade é o conjunto-solução $S$ ; que é o conjunto cujos elementos solucionam a equação proposta, isto é, são soluções dela. Como $S$ tem mais de um elemento e a equação está na forma de um polinômio, já sabemos que ele não pode ser do primeiro grau, já que pelo Teorema Fundamental da Álgebra uma equação polinomial de grau $n$ tem exatamente $n$ soluções complexas (no conjunto dos números complexos) e no máximo $n$ soluções reais (em $\mathbb{R}$ ).

(3) Entendido isso, podemos trabalhar sobre a incógnita como sendo $X$ . Assim, colocando $X^2$ em evidência, teremos:

$X^2 \cdot (X^2 - K) = 0$

Para que um produto de dois números seja nulo, é necessário que pelo menos um deles seja zero. Assim, sabemos que $X^2 = 0$ , logo $X = 0$ , caracterizando duas raízes reais e iguais a zero; ou $X^2 - K = 0$ , daí:

$X^2 = K \Rightarrow X = +\sqrt{K} \quad \textrm{ou} \quad X = -\sqrt{K}$

Ou seja, temos um conjunto solução, que chamaremos de $S'$ representado por $S'= \{-\sqrt{K}; 0; +\sqrt{K}\}$ , que pressupõe necessariamente que $K \geq 0$ .

Como $S = S'$ devemos ter exatamente os mesmos elementos em ambos, ou seja $\sqrt{K} = 9$ . Portanto, para $K \geq 0$ , sabemos que $K = 81$ . Teremos, então a opção B.

Assim, pra fecharmos o assunto, é necessário fazer algumas considerações importantes:

Verificar sempre quem é a incógnita da equação;
Verificar quem é o conjunto universo no qual se está trabalhando. No osso caso consideramos o conjunto dos números reais $\mathbb{R}$ , mas poderíamos ter os naturais $\mathbb{N}$ , inteiros $\mathbb{Z}$ , complexos $\mathbb{C}$ , etc;
É importante entender o papel do conjunto-solução em uma equação; e
Cuidado com equações literais.

É isso, espero ter respondido a dúvida da Helena e de outras pessoas, mesmo com um “certo” atraso.

Vídeo sobre conjunto-solução em nosso canal:

Minha iniciativa é gratuita.

Você pode ajudar doando qualquer quantia via PIX: leonardosantos.inf@gmail.com

Fique a vontade, qualquer ajuda é bem vinda! E a melhor ajuda que você pode dar não custa nada: só basta divulgar esta iniciativa!

Até!

[LSB]

Uma Pequena Lista Sobre Funções (e uma “Pitada” de Conjuntos)…

Segue uma pequena lista de 10 exercícios envolvendo o assunto funções do primeiro grau, com um pequeno adendo de conjuntos numéricos. Clique no link a seguir e divirta-se:

Funcao_1_Grau_VIII

Bons estudos e sucesso!

@LSBar – CEO

Conjuntos: Intervalos de Números Reais

Nesta vídeo aula falamos sobre os intervalos de números reais e suas representações algébricas e geométricas. Abordamos intervalos com limites abertos e fechados.

Seja Patrão! Ajude-nos doando $1 e tenha acesso a conteúdo exclusivo, inscrevendo-se em nosso PATREON:
http://www.patreon.com/mentor

Veja muitos exercícios (com gabarito) sobre este assunto em:
Matemática: https://cursomentor.com/matematica-2/
Física: https://cursomentor.com/fisica/

Veja também muitos exercícios de outros assuntos indo em: http://www.cursomentor.com

Curta nossa fanpage: http://www.facebook.com/cursomentor

Siga-nos no Twitter:
http://www.twitter.com/curso_mentor

Bons estudos e sucesso.

Conjuntos: Números Reais

Olá alunos, fechando a série de conjuntos numéricos, trazemos um vídeo sobre os números reais e mostramos como eles se relacionam com os demais conjuntos: naturais, inteiros, racionais e irracionais.

Seja Patrão! Ajude-nos doando $1 e tenha acesso a conteúdo exclusivo, inscrevendo-se em nosso PATREON:
http://www.patreon.com/mentor

Veja muitos exercícios (com gabarito) sobre este assunto em:
Matemática: https://cursomentor.com/matematica-2/
Física: https://cursomentor.com/fisica/

Veja também muitos exercícios de outros assuntos indo em: http://www.cursomentor.com

Curta nossa fanpage: http://www.facebook.com/cursomentor

Siga-nos no Twitter:
http://www.twitter.com/curso_mentor

Bons estudos e sucesso.

Conjuntos: Números Irracionais

Mais um vídeo aqui em nosso canal. Desta vez trazemos um vídeo sobre os números irracionais. Falamos um pouco sobre as dízimas não periódicas e sobre a definição de um número irracional.

Seja Patrão! Ajude-nos doando $1 e tenha acesso a conteúdo exclusivo, inscrevendo-se em nosso PATREON:
http://www.patreon.com/mentor

Veja muitos exercícios (com gabarito) sobre este assunto em:
Matemática: https://cursomentor.com/matematica-2/
Física: https://cursomentor.com/fisica/

Veja também muitos exercícios de outros assuntos indo em: http://www.cursomentor.com

Curta nossa fanpage: http://www.facebook.com/cursomentor

Siga-nos no Twitter:
http://www.twitter.com/curso_mentor

Bons estudos e sucesso.