Olá leitor.
Hoje trazemos um problema que envolve um sistema de equações não lineares e que, a princípio, parece fácil, mas na realidade, envolve métodos mais sofisticados que simplesmente substituir uma equação na outra. Veja o problema a seguir:
Sejam  ,
, 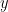 e
e  números complexos que satisfazem o sistema de equações abaixo:
números complexos que satisfazem o sistema de equações abaixo:

O valor da soma  é:
é:
a) 
b) 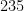
c) 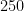
d) 
e) 
Enviada por Matheus
Podemos inicialmente pensar em um polinômio 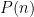 tal que
tal que  ,
, 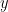 e
e  sejam exatamente suas raízes e seja escrito como:
sejam exatamente suas raízes e seja escrito como:

Das relações de Girard e do sistema dado chegamos a:
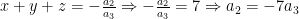
Alem disso, sabendo que 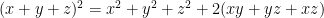 , portanto:
, portanto:
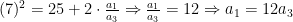
Da última equação do sistema:
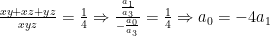
Ou seja 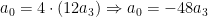 . Finalmente, podemos usar as somas de Newton:
. Finalmente, podemos usar as somas de Newton:
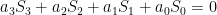
Teremos:
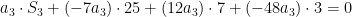
Como  , temos:
, temos:

Chegando à opção B.
Como observação, não nos estendemos sobre as somas de Newton, mas o faremos em momento oportuno!!!
Até a próxima!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
https://apoia.se/mentor
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]