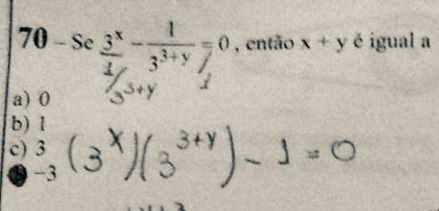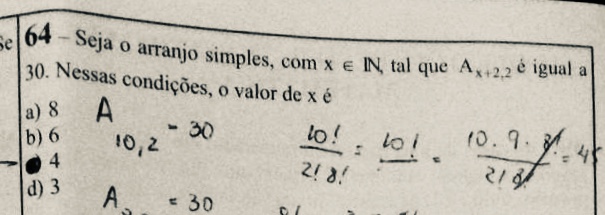Olá, nesta postagem queremos trazer um exemplo de problema que exige o conhecimento, mesmo que básico sobre os principais pontos notáveis do triângulo. Em particular, estamos falando sobre o incentro. Em vez de apenas resolver o problema, queremos falar um pouco sobre este ponto notável, aproveitando como uma revisão básica.

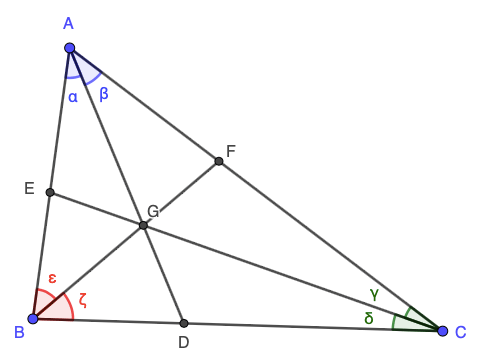
Por definição, o incentro é o ponto de encontro das bissetrizes internas de um triângulo. As bissetrizes internas de um triângulo são segmentos que tem um extremo sendo o vértice do triângulo e o outro vértice sobre o lado do triângulo, ou seja é uma ceviana.

Na figura anterior, no triângulo , , e são cevianas. Se tivermos , e então as três cevianas serão bissetrizes internas.

Uma observação importante aqui: não estamos provando que as três bissetrizes internas concorrem (se interceptam) no mesmo ponto (isto ficará pra outro momento…), mas por ora, vamos admitir que seja verdade, já que, da fato, é.

Assim, feita esta breve observação e “dados nomes aos bois” chamaremos o ponto o de incentro do triângulo . E, claro, pela própria construção da figura, é intuitivo que o incentro é sempre interno ao triângulo, seja ele acutângulo, retângulo ou obtusângulo.

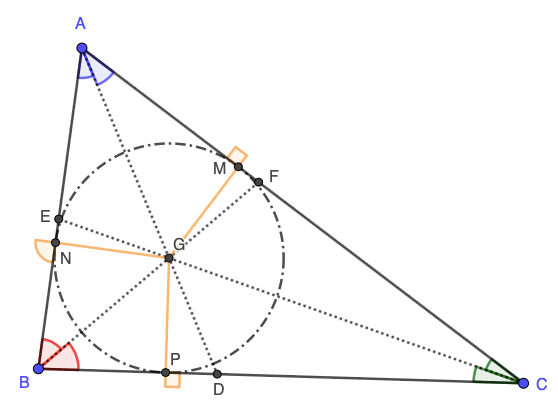
Por uma questão de simplificação, vamos convencionar que ângulos de mesma cor têm a mesma medida. Sabendo que tangentes comuns traçadas de um mesmo ponto a uma circunferência são iguais, o incentro de um triângulo é o centro do círculo inscrito no mesmo triângulo.

Assim, na figura anterior, os ângulos em laranja são todos retos (valem ) e , em que é o raio do círculo inscrito, também chamado de incírculo. Fiz essa figura pra que seja percebido que os “pés” das bissetrizes não são, necessariamente, pontos do círculo inscrito.

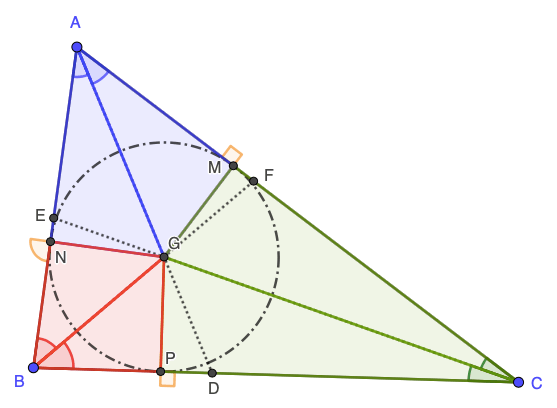
Esta figura traz várias consequências implícitas. Por exemplo, os triângulos de mesma cor na figura a seguir, são congruentes. Mostrando, por exemplo que , e .

Assim, veja que o incentro está a uma mesma distância de cada um dos lados do triângulo.

Com base nesta figura, só para citar uma propriedade importante, podemos mostrar que . Como não é nosso foco, fica pra depois. Bom qual nosso foco, no momento então? A relação entre o angulo interno do vértice e o ângulo na figura a seguir:

Veja que é o incentro, pois e são bissetrizes internas. Assim, teremos as seguintes relações:

para o triângulo

e também

Fica, então, simples de se perceber que:

Ou seja:

ou

Vamos então ao problema proposto na EEAr há algum tempo, que trago aqui com uma ligeira adaptação:

(EEAr — Modificada)

Um triângulo tem com incentro. Se , qual o valor de ?

a)

b)

c)

d)

Veja que o problema trata exatamente do que acabamos de ver. Como é incentro, basta fazermos:

Assim:

Portanto, letra D.

Ah, e aqui está um vídeo sobre todos os pontos notáveis do triângulo.

Espero ter esclarecido um pouco mais sobre o incentro e suas propriedades.

Minha iniciativa é gratuita.

Você pode ajudar doando qualquer quantia via PIX: leonardosantos.inf@gmail.com

Fique a vontade, qualquer ajuda é bem vinda! E a melhor ajuda que você pode dar não custa nada: só basta divulgar esta iniciativa!

Até!

[LSB]