Teorema do Impulso. Você sabe aplicar?

Um teorema comum utilizado em física básica afirma que o impulso causado por uma força equivale a variação de seu momento linear. A questão a seguir da Mackenzie usa este teorema de forma interessante.

(MACK-SP) Um corpo em repouso e de $1,0$ t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo ( $t$ ) segundo a função $F = 200 t$ , no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante $t = 10$ s vale:

a) $3,6$ km/h.

b) $7,2$ km/h.

c) $36$ km/h.

d) $72$ km/h.

e) $90$ km/h.

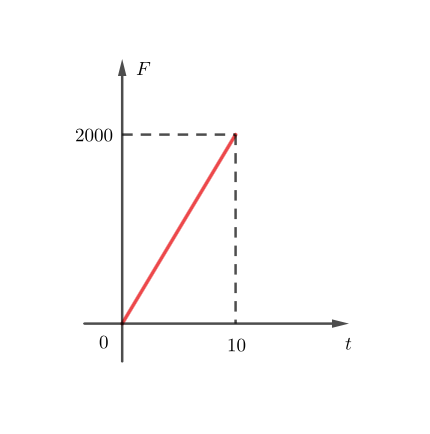
O mais importante é perceber que a força, nesse caso é variável, dada por $F(t) = 200t$ , ocasionando o gráfico abaixo:

Assim, precisamos usar a força média, uma vez que o impulso total de uma força é igual a variação da quantidade de movimento (ou do momento linear). Repare que, neste caso, a direção da força é constante, facilitando parcialmente nossa análise.

Assim, teremos:

$\int_0^t \vec{F}\,dt = \Delta \vec{Q}$

Ou seja, a área abaixo do gráfico $F \times t$ é igual à variação de momento linear unidimensional (em uma única direção). Daí, como $F = 200t$ e $t = 10$ s, teremos $F = 2000$ N e, por conta disso: