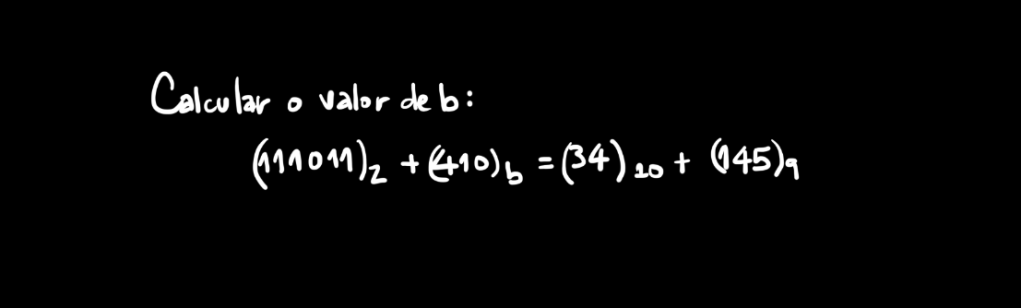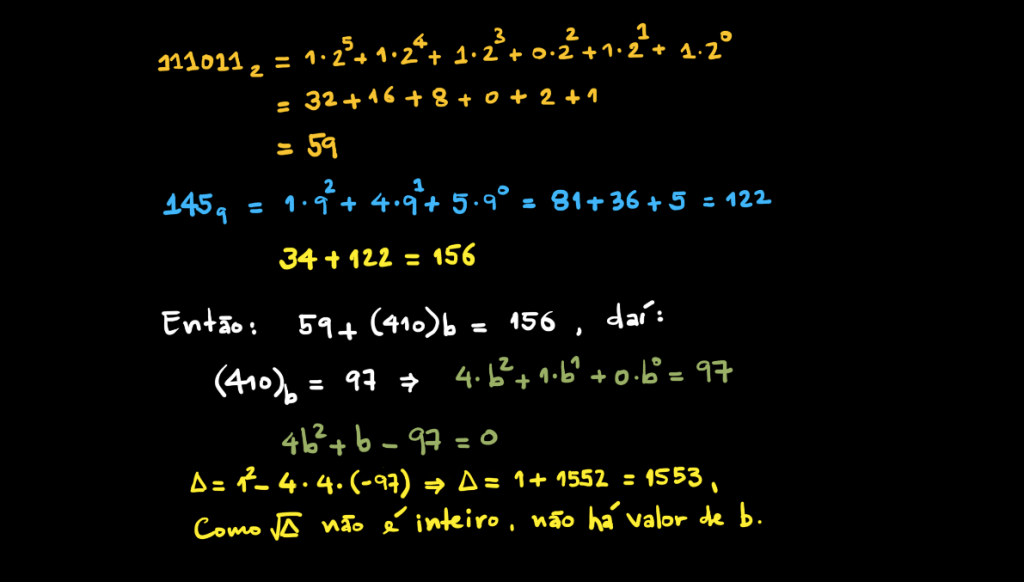Vamos a solução de mais um problema da semana. Eis o enunciado da última semana:
Sendo
calcule o valor de
.
Primeiro. vejamos que e que
; com isso, teremos:
como e
podemos escrever:
Arranjando os termos:
Portanto:
Agora, elevando ambos os membros a , ficamos com:
Estamos quase lá, pois agora temos . Elevando ambos os lados a
:
Ou seja, , assim a resposta é
ou
.
Resolveram este problema:
- Micael França.
Listagem de problemas resolvidos até agora:
- (4) Micael França
- (3) Ygor Gabriel
- (2) Yasmim Silva
- (2) Ygor Farias
- (2) Arthur Rocha
- (2) @mariopersico_
- (2) Iuri Henrique
- (1) Alef
- (1) Lucca Gabriel
- (1) Gustavo
- (1) Lucas Lopes
- (1) Davi do Nascimento Teles Barata
- (1) Enzo Botarelli