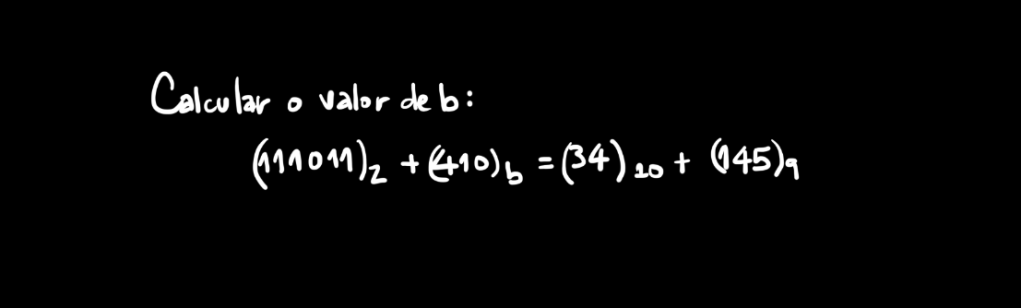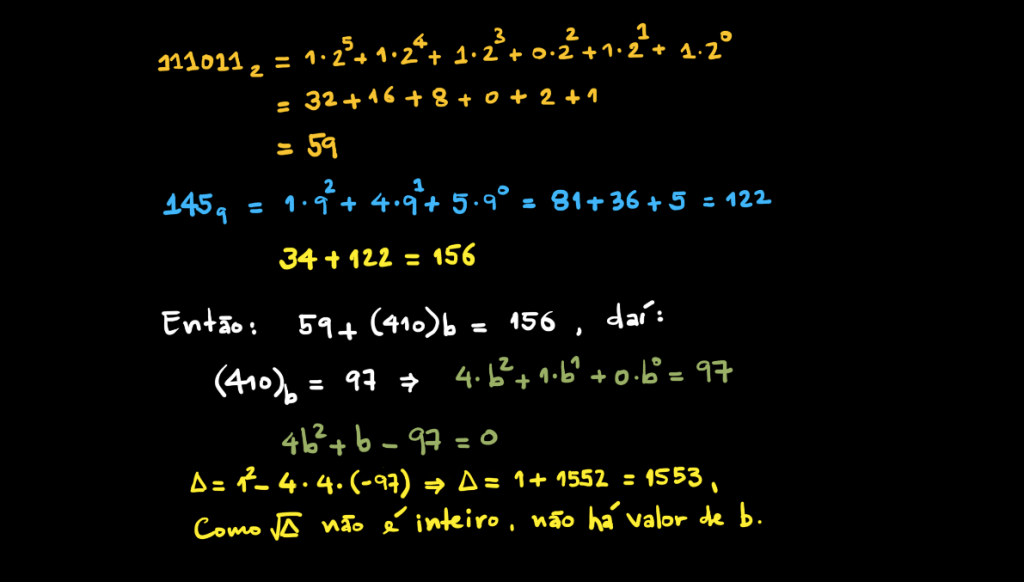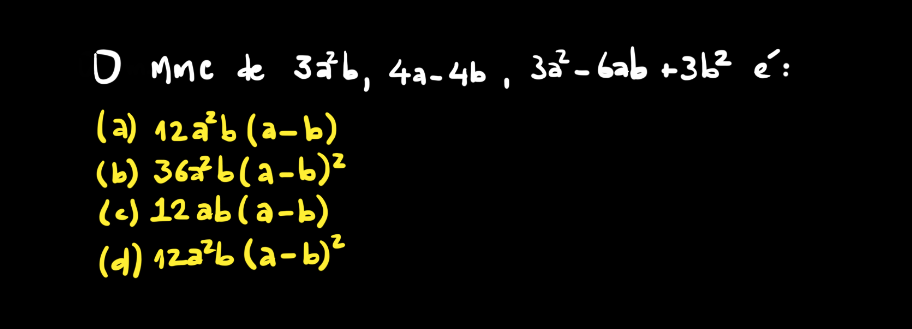Tira-Teima #1

Problema da Semana #12: Potências

Vamos a mais um problema da semana, desta vez proposto pelo ilustríssimo mentor Paulo de Sousa Sobrinho, mais conhecido por Paulinho. Segue o enunciado:

Sendo $x + \frac{1}{x} = \sqrt{2}$ , calcular o valor de $x^{2021} + \frac{1}{x^{2021}}$ .

Agora é com você , mãos a obra e nos vemos em breve, na próxima solução.

Até lá.

[LSB]

Problema da Semana #11: Solução Sem Logaritmos!

$Expressão$

Vamos a solução de mais um problema da semana. Eis o enunciado da última semana:

Sendo $147^x = 189$ calcule o valor de $7^{\frac{1-2x}{3(x-3)}}$ .

Primeiro. vejamos que $147 = 21 \cdot 7$ e que $189 = 27 \cdot 7$ ; com isso, teremos:

$(21 \cdot 7)^x = 27 \cdot 7$

como $21 = 3 \cdot 7$ e $27 = 3^3$ podemos escrever:

$3^x \cdot 7^x \cdot 7^x = 3^3 \cdot 7^1$

Arranjando os termos:

$\frac{3^x}{3^3} = \frac{7^1}{7^{2x}}$

Portanto:

$3^{x-3}= 7^{1 - 2x}$

Agora, elevando ambos os membros a $\frac{1}{x-3}$ , ficamos com:

$(3^{x-3})^{\frac{1}{x-3}}= (7^{1 - 2x})^{\frac{1}{x-3}}$

Estamos quase lá, pois agora temos $3 = 7^{\frac{1 - 2x}{x-3}}$ . Elevando ambos os lados a $\frac{1}{3}$ :

$3^{\frac{1}{3}} = (7^{\frac{1 - 2x}{x-3}})^{\frac{1}{3}}$

Ou seja, $3^{\frac{1}{3}} = 7^{\frac{1 - 2x}{3(x-3)}}$ , assim a resposta é $3^{\frac{1}{3}}$ ou $\sqrt[3]{3}$ .

Resolveram este problema:

Micael França.

Listagem de problemas resolvidos até agora:

(4) Micael França
(3) Ygor Gabriel
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata
(1) Enzo Botarelli

Existe o Valor de b?

Estamos de volta com mais uma dúvida enviada para nós.

O problema em questão trata de sistemas de numeração. Neste caso, além da base $10$ há outras bases envolvidas.

A solução segue na imagem abaixo:

Veja que não é possível, uma vez que $b$ não será um número inteiro.

Até a próxima.

[LSB]

Problema da Semana #11: Tente Calcular o Valor da Expressão

Segue o problema proposto, mais uma vez pelo grande mentor, José Maria Gomes; o grande China.

Sendo $147^x = 189$ calcule o valor de $7^{\frac{1-2x}{3(x-3)}}$ .

Um problema envolvendo as meras propriedades de potenciação.

Este é um assunto muito importante para todos os alunos que farão um concurso no qual a álgebra elementar é cobrada. Agora é com você! Acha que consegue? Mãos a obra.

Até a solução!

[LSB]

Problema da Semana #10: Uma Solução Mais ou Menos Simples

Segue a solução do problema da semana #10. Vamos relembrar o enunciado.

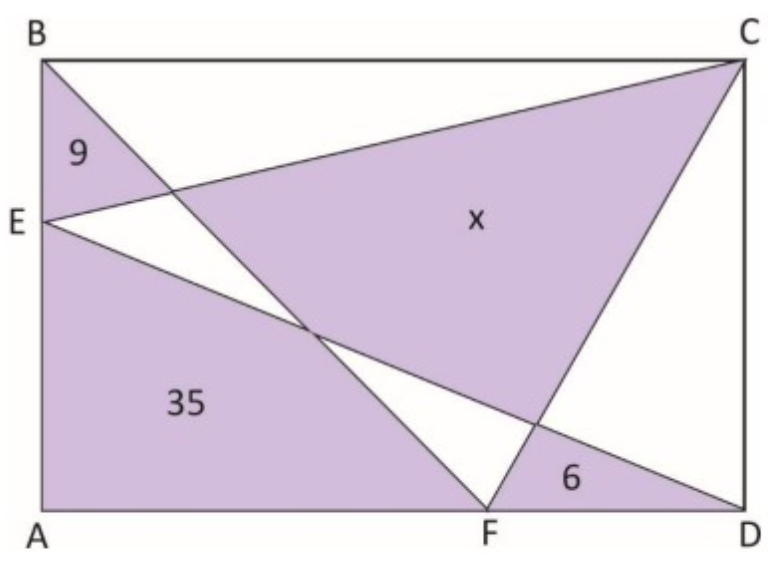
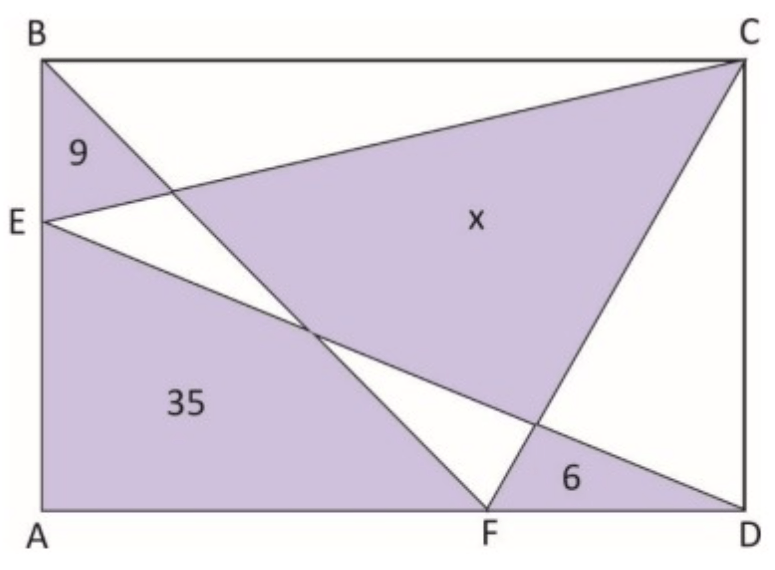
Na figura abaixo, o terreno retangular $ABCD$ foi loteado e os números que aparecem no interior de alguns destes lotes, indicam suas respectivas áreas em $\text{km}^2$ .

A medida da área indicada pelo lote da letra $x$ , em $\text{km}^2$ é igual a:

a) $70$

b) $40$

c) $60$

d) $50$

e) $54$

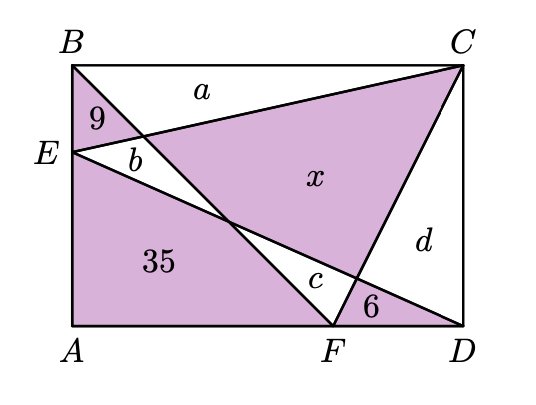
Uma solução “simples” é chamar a áreas desconhecidas em branco de $a$ , $b$ , $c$ e $d$ . Como na figura abaixo:

Perceba que a área do triângulo $BCF$ é igual à área do triângulo $CDE$ , pois ambos são iguais a metade da área do retângulo (esse pode ser um fato difícil de perceber, pense um pouco até que isso fique claro para você). Assim, podemos escrever:

$a+x + c = b + x + d \Leftrightarrow a+c = b+d$

Pelo mesmo motivo teremos:

$9 + b + 35 + 6 + d = a + x + c \Leftrightarrow 50 + \underbrace{b + d}_{= a+c} = x + a + c$

Logo $x = 50$ . Há outra solução usando o Teorema dos Carpetes. Mas essa deixaremos para o grande mentor José Maria Gomes (o famoso China).

Resolveram este Problema:

Micael França

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(3) Micael França
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata
(1) Enzo Botarelli

Se seu nome não apareceu, me avise pois pode ser que eu não tenha visto a sua solução enviada.

Bora pra cima!

O Mínimo Múltiplo Comum (M.M.C.) de Expressões Algébricas: uma Questão da EEAr

Um aluno mandou uma dúvida sobre este assunto que compartilho com vocês agora. Ela trata sobre o MMC de expressões algébricas que caiu na prova da EEAR. Essa é uma questão antiga deste concurso e, atualmente, dificilmente aparecia algo nesse sentido já que o edital se concentra mais em assuntos do ensino médio atualmente.

Apesar disso, este é um assunto muito comum em provas militares (principalmente as que envolvem o conteúdo do 9º ano, tais como CN, EPCAr e Colégios Militares em geral…) e para resolvê-lo, em geral, precisamos única e exclusivamente da definição do que significa o calcular o mínimo múltiplo comum (ou MMC).

A imagem do enunciado da questão segue abaixo.

Como disse, basta aplicar a definição de MMC neste caso. Lembre-se que antes de verificar a solução logo abaixo, seria legal tentar resolver.

Veja que aparece também uma fatoração algébrica envolvendo o quadrado de uma diferença – que é um produto notável. Como falei, trata-se de uma questão simples (o que, via de regra nem sempre é fácil…), no sentido de que, conhecida a definição de MMC, o resto torna-se banal.

Ainda tem dúvida? Mais questões como essa? Conte-nos nos comentários e, até a próxima!

[LSB]

O Carnaval Acabou… Mas a Folia da Divisibilidade… Não!

O carnaval de 2025 termina hoje (dia 5/3/2025), mas trazemos mais uma pequena lista envolvendo a divisibilidade dos números naturais com questões do Colégio Naval de vários anos diferentes: é sua chance de botar novamente o bloco “Unidos da Divisibilidade” (isto é que é um verdadeiro trocadilho matemático!) na avenida mais uma vez.

Segue a lista com as questões.

4_3_MAT_9_1_MIL_Divisibilidade_LNS Baixar

O Colégio Naval adora este assunto e nada mais eficiente do que praticar em cima dele para se aprimorar. Use tudo o que estiver a mão, principalmente as propriedades do resto em relação a uma divisão de naturais. Nesta lista ainda incluímos uma breve questão de geometria plana para dar aquela variada. Mas é simples ~~(ou não…)~~ pode confiar.

Tente resolver estas questões e depois me diga nos comentários se achou simples demais. Afinal, a folia não pode parar.

Até a próxima!

[LSB]

Problema da Semana #10: Calcule a Área Desconhecida!

Nesta semana trazemos um problema proposto pelo grande mestre José Maria Gomes (vulgo China), autor do livro Tópicos de Matemática IME-ITA-Olimpíadas cujas capas encontram-se abaixo:

O problema trazido por ele tem o enunciado que segue abaixo:

Na figura abaixo, o terreno retangular $ABCD$ foi loteado e os números que aparecem no interior de alguns destes lotes, indicam suas respectivas áreas em $\text{km}^2$ .

A medida da área indicada pelo lote da letra $x$ , em $\text{km}^2$ é igual a:

a) $70$

b) $40$

c) $60$

d) $50$

e) $54$

E aí? Acha que consegue resolver essa? Responda nos comentários e/ou mande para mim sua solução marcando com #semana10 para que eu possa identificar sua resposta rapidamente.

Mãos à obra e bora resolver mais este problema.

Até mais.

[LSB]

Problema da Semana #9: Solução e a Proposta de um Novo Problema

Estamos de volta para falar do problema da semana #9 e trazer sua solução, bem como os nomes dos que solucionaram e também para fazer algumas considerações gerais.

Relembrando o problema, o enunciado era o seguinte:

(AMAN — 1984) Calcular a soma das raízes da equação:

$2^{x^2} = 32(2^{3x-7})$

a) $3$

b) $2$

c) $-3$

d) $-2$

e) N.R.A.

Como podemos ver, esse é um problema da Academia Militar das Agulhas Negras (AMAN), e envolve uma espécie de equação exponencial. Como a base é $2$ , basta que os expoentes sejam iguais para que a igualdade seja verificada. Então, teremos:

$2^{x^2} = 2^5 \cdot 2^{3x - 7} \Leftrightarrow 2^{x^2} = 2^{5 + 3x - 7}$

Portanto:

$2^{x^2} = 2^{3x - 2} \Leftrightarrow x^2 = 3x - 2 \Leftrightarrow x^2 - 3x + 2 = 0$

Como queremos apenas a soma das raízes e não as raízes em si, basta calcular a soma que vale $S = -\frac{-3}{1} = 3$ . Caso você quisesse achar as raízes bastaria verificar que: