Introdução

Se a matemática já é a vilã das disciplinas para muita gente, este sem dúvida é um dos temas que mais atormenta e dificulta a vida das pessoas que estão estudando matemática básica.

As operações com frações modificam um pouco a forma de lidar com os números uma vez que a notação usada é diferente dos numerais “comuns” e isto, certamente, é apenas uma das barreiras ao aprendizado das operações com frações.

Para ajudar a diminuir um pouco esta dificuldade e ajudar muita gente, decidi escrever este texto que esclarece alguns pontos importantes sobre as frações. Mas antes de começar, quero deixar claro que, aqui, estamos falando para pessoas que já tiveram contato com números inteiros e entendem o significado de escrever um número negativo tal como . Então vamos lá.

A primeira coisa que quero esclarecer é que o sinal de menos em uma fração pode ficar no numerador (“em cima”), no denominador (“embaixo”) ou “a frente” da fração que o resultado representa a mesma fração. Por exemplo, é o mesmo que 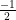que é o mesmo que .

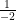Agora vamos ao que interessa.

Adição/Subtração de Frações com o Mesmo Denominador

Se duas ou mais frações possuem o mesmo denominador, podemos operar apenas com os numeradores e repetir o denominador no resultado final:

Exemplo:

Repare que escrever é o mesmo que escrever . As regras de operações e suas prioridades de acordo com sinais de associação (parenteses, colchetes e chaves) devem ser mantidas. Vamos à mais um exemplo:

Exemplo:

Resolvendo a operação dentro dos parenteses teremos:

Continuando:

Adição/Subtração de Frações com Denominadores Diferentes

Quando os denominadores são diferentes, aí o processo é um pouco mais longo. Primeiro precisamos igualar os denominadores. Mas como? Existe um conceito importante no estudo das frações chamado de frações equivalentes.

Duas frações são ditas equivalentes se representam a mesma parte do todo, isto é, de uma mesma unidade retiramos ou usamos a mesma quantia total. Vamos exemplificar. Se você divide uma pizza em dois pedaços iguais e pega um, neste caso 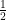, você terá exatamente a mesma quantia total que se dividi-la em quatro pedaços e pegar dois, ou seja . Logo:

Mas como obtemos frações equivalentes? Simples. Multiplicando (ou dividindo) o numerador e o denominador pelo mesmo fator. Veja que ao usar a fração  podemos obter frações equivalentes:

Poderíamos também fazer:

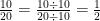
Assim, podemos sempre uma fração equivalente a uma fração dada. Por exemplo, suponhamos que você quisesse resolver o seguinte problema:

Encontrar uma fração equivalente a 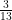com denominador .

Para resolvê-lo, basta verificar por qual fator devemos multiplicar 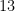para obtermos . É claro que basta fazer e, depois, multiplicar numerador e denominador por este fator:

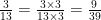
Então, afinal, como podemos operar com frações de denominadores diferentes? Encontrando frações equivalentes para cada uma delas de modo que todas tenham o mesmo denominador. A maneira mais simples de fazer isso é escolher frações equivalentes as primeira com um denominador que é igual ao produto dos denominadores das frações originais. Por exemplo, vamos escrever duas frações respectivamente equivalentes a 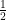e .

Como vimos, podemos usar como o novo denominador de cada uma. Agora a pergunta é: e o novo numerador de cada fração? Para saber o novo numerador, de modo que a nova fração seja equivalente a anterior, multiplicamos o numerador antigo pelo resultado da divisão do novo denominador pelo velho denominador:

Assim, para a fração 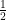, como o novo denominador é 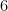, temos  e este fator multiplica o antigo numerador, resultando na fração 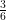, veja que 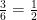. Fazendo o mesmo para a fração , teremos 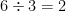e a nova fração será .

Fica então fácil efetuar a conta 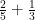. Como vimos, o primeiro passo é encontrar o denominador comum que pode ser o produto dos antigos denominadores: . Agora dividimos por cada denominador antigo e multiplicamos o respectivo resultado pelo antigo numerador de cada uma, obtendo novas frações, porém equivalentes às primeiras, veja:

E:

Agora, e para três ou mais frações? Podemos usar o mesmo processo. Vejamos o exemplo a seguir.

Exemplo: Calcular o valor de .

Vamos ao processo. Primeiro, multiplicar os denominadores:

Agora dividimos este valor por cada denominador e multiplicamos o resultado pelo respectivo numerador, obtemos então:

Continuando:

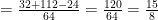
Usando o m.m.c.

O método apresentado funciona, sempre. Porque decorre da definição de fração equivalente. Mas pode ser trabalhoso, principalmente se os denominadores forem números de maior grandeza. Experimente o método anterior para resolver a seguinte expressão:

Certamente, você terá algum trabalho, pois . Assim, podemos usar o mínimo múltiplo comum entre os denominadores para achar um novo denominador o que diminui consideravelmente o esforço. Veja que 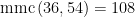. Portanto o novo denominador é e podemos seguir como anteriormente:

 Assim, o processo usando o mínimo múltiplo comum torna a conta menor e, de certa maneira, facilita-o. Vamos retomar um exemplo anterior para ilustrar a facilidade de usar o m.m.c:

Exemplo: Calcular o valor de .

Como é múltiplo de e , o 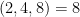e podemos seguir como antes, com o novo denominador sendo .

Repare que as contas são muito “menores” neste caso.

Conclusão

Dá para automatizar este processo, ou seja, existe uma fórmula? Sim, podemos escrevê-la como segue:

Claro que, aqui, consideramos . E, ainda, se houver mais que duas frações, basta agrupá-las de duas em duas e fazer o mesmo acima.

Se quiser fazer exercícios sobre este assunto vá até a nossa página de exercícios. Lá você encontrará destes e de muitos outros.

Tem dúvida, sugestão ou reclamação? Mande-nos um e-mail: mentor.contato@gmail.com.

Até.

[LSB]