Mais uma dúvida resolvida. Segue o enunciado:
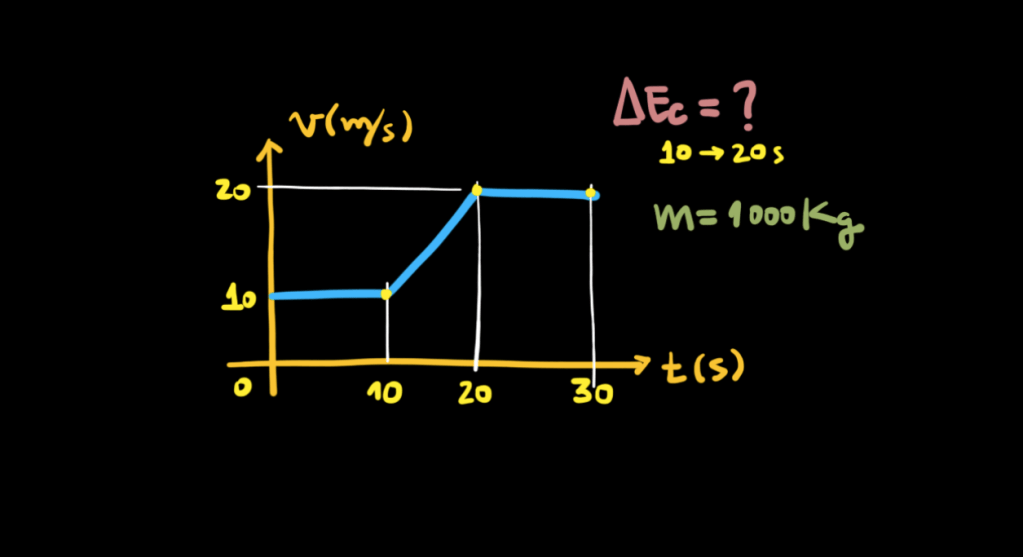
Queremos a variação da energia cinética entre os instantes e
s. A massa vale
kg. Então:

Nossa loja de camisetas: http://reserva.ink/equilateral







Outros conteúdos:
Até a próxima!
[LSB]
Mais uma dúvida resolvida. Segue o enunciado:

Queremos a variação da energia cinética entre os instantes e
s. A massa vale
kg. Então:

Nossa loja de camisetas: http://reserva.ink/equilateral







Outros conteúdos:
Até a próxima!
[LSB]
Olá caros alunos e estimados leitores. Segue uma pequena lista com 10 problemas de física e suas respectivas soluções.
Ela serve de base para você que está iniciando seus estudos na cinemática escalar, haja vista que este é um tema presente, se não em todos, em praticamente todos os concursos nos quais a física é uma das disciplinas.
Veja abaixo a lista de exercícios com as suas dez questões:
Seguem abaixo as soluções de cada um dos problemas que aparecem na lista.
Espero que seja útil a você.
Compre nossas camisetas indo em: http://www.reserva.ink/equilateral
Siga-nos no Instagram: @projeto.mentoria_
Bons estudos e até a próxima!
[LSB]
Um dos assuntos iniciais do estudo da física para os alunos do ensino médio concentra-se na área que envolve a medida das temperaturas bem como o conceito físico de calor.
Como quase tudo no estudo de física, muitas vezes o conhecimento popular — o famoso senso comum — não bate com o conhecimento físico correto do assunto e, por isso, muitas pessoas acabam por errar problemas que envolvem conceitos simples no estudo desta disciplina.
Questionamentos como “… o que significa dizer que algo está “quente” ou “frio”?” costumam confundir-se com a ideia física de receber (ou ceder) energia térmica e isso, pode ou não atrapalhar o entendimento de certos problemas principalmente quando se trata de Termologia, a grande área da qual trata este assunto.
Além desse tema inicial, é importante conhecer assuntos que envolvem as escalas termométricas e a conversão mútua entre essas escalas de forma que se possa expressar a medida dessa temperatura em diversas escalas distintas, já que umas são mais ou menos usuais do que outras.
Ademais, há o conceito de equilíbrio térmico e a Lei Zero da Termodinâmica, bem como a comparação das variações de temperatura entre escalas, algo também muito abordado neste assunto.
Tendo tudo isso em mente, assista essa aula que fala sobre isso:
E aqui tem uma lista de exercícios para treinar sobre o assunto:
Finalizando é o de sempre… tendo dúvidas, procure-nos!
Até a próxima!
[LSB]
No último sábado dia 8/3, eu fiz uma aula breve sobre Introdução à Física, na qual falamos sobre o que é a Física, a nossa ciência dos fenômenos naturais, ou seja, aqueles que ocorrem na natureza.
Nesta aula, falamos sobre as grandezas físicas escalares (bem definidas pelo módulo) e também as vetoriais (que dependem do módulo, da direção e do sentido para ficarem bem definidas) além de dar exemplos de cada e comentei também um pouco sobre o Sistema Internacional de Unidades o famoso S.I.
Falamos brevemente sobre a notação científica que corresponde a escrever um número no formato com
e, além disso sobre a ordem de grandeza, que será
, se
em módulo; e,
, se
; além, claro de, mais uma vez, dar exemplos.
No fim de tudo, resolvemos uns exercícios da EEAr sobre estes assuntos.
O vídeo da aula segue abaixo caso você queira ser um APROVADO (ou fique de preguiça…!).
Além desta inoxidável aula (já dizia o grande “Rei do Elogio”…), segue também uma pequena lista de exercícios para enriquecer ainda mais seu conhecimento sobre o assunto:
Minha sugestão é que você tente resolver esta lista como um pequeno simulado sobre o assunto, verificando se tudo ficou bem fundamentado. Use a aula como apoio e, qualquer dúvida, não hesite em colocar nos comentários.
Um grande abraço e até a próxima!
[LSB]
Na última postagem falamos sobre um problema cuja solução envolvia o impulso e a quantidade de movimento (ou momento linear). Mas será que há outra solução? E a resposta é: sim! Há outra solução. Mas antes vamos relembrar qual o enunciado. Segue:
(MACK-SP) Um corpo em repouso e de
t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo (
) segundo a função
, no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante
s vale:
a)
km/h.
b)
km/h.
c)
km/h.
d)
km/h.
e)
km/h.
Vamos fazer o seguinte: primeiro vamos encontrar o formato da aceleração em função do tempo, que neste caso, obviamente, não será constante:
Como kg, teremos
(S.I.), cujo gráfico segue na imagem a seguir.
Agora vem uma parte importante: como a área entre o gráfico de
em função do tempo e o eixo horizontal representa a variação de velocidade. Em outras palavras, se
, então
e:
Que representa a variação de velocidade entre os instantes e
. Assim, a área será de
m/s ou
km/h. Veja que na integral teríamos o mesmo:
m/s
Assim, é possível termos o mesmo valor final usando tanto a integral quanto apenas a área abaixo da curva .
Esta solução foi proposta por Diego Gorito, com algumas adaptações minhas para incluir a parte de cálculo e atende ao Matheus Teixeira que queria uma solução que não envolvesse o impulso.
Até próxima pessoal!
[LSB]
Um teorema comum utilizado em física básica afirma que o impulso causado por uma força equivale a variação de seu momento linear. A questão a seguir da Mackenzie usa este teorema de forma interessante.
(MACK-SP) Um corpo em repouso e de
t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo (
) segundo a função
, no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante
s vale:
a)
km/h.
b)
km/h.
c)
km/h.
d)
km/h.
e)
km/h.
O mais importante é perceber que a força, nesse caso é variável, dada por , ocasionando o gráfico abaixo:
Assim, precisamos usar a força média, uma vez que o impulso total de uma força é igual a variação da quantidade de movimento (ou do momento linear). Repare que, neste caso, a direção da força é constante, facilitando parcialmente nossa análise.
Assim, teremos:
Ou seja, a área abaixo do gráfico é igual à variação de momento linear unidimensional (em uma única direção). Daí, como
e
s, teremos
N e, por conta disso:
Ou seja, a velocidade final é de m/s e, finalmente, passando para km/h teremos
km/h. Opção C.
E aí, acertou essa?
Se sim, parabéns; se não, bora para a próxima!
[LSB]
Existem muitos problemas de cinemática elementar que são muito difíceis. Especialmente quando os cronômetros de dois objetos não estão sincronizados, fazendo com que seus instantes iniciais de contagem de tempo sejam diferentes.
Trazemos então o seguinte problema, do ITA, um vestibular extremamente difícil que exige um alto nível de conhecimento de seus candidatos nas áreas de Matemática, Física, Química, Língua Portuguesa e Lingua Inglesa. Segue o enunciado do problema:
Um móvel
parte da origem
, com velocidade inicial nula, no instante
e percorre o eixo
com aceleração constante
. Após um intervalo de tempo
, contado a partir da saída de
, um segundo móvel
parte de
com uma aceleração igual a
, sendo
.
alcançará
no instante:
a)

b)

c)
d)
e)
O móvel move-se a partir do repouso com aceleração
, o que ocorre durante um
, ou seja, seus espaços em função do tempo ficam dados pela equação:
Para o móvel teremos:
Sabemos que o móvel partiu do repouso, portanto
e queremos saber em que instantes
e
se encontrarão, ou seja, quando teremos
, assim:
Como e
partem do mesmo ponto temos
e, então:
Agora faremos uma suposição crucial: a de que , admitindo que
também partiu do repouso, daí:
Então, como , teremos:
Simplificando em ambos os membros teremos:
Chegamos onde queríamos. Veja que e que
, ou seja,
. Por outro lado,
e
, portanto
; assim:
Finalmente, podemos escrever: . Ou como aparece nas opções:
Opção E.
O problema foi enviado por Arthur Rocha.
Até a próxima.
[LSB]
Alguns Links úteis:

Eu sou Leonardo Santos e você veio ao lugar certo pra aprender!
Está é uma iniciativa para trazer materiais de boa qualidade até você e te ajudar a aprender mais.
Vamos crescer mais! Faça parte:
— Doe via PIX: leonardosantos.inf@gmail.com
— Siga-nos nas redes:
Instagram: http://www.instagram.com/mentorblog_oficial
Facebook: https://www.facebook.com/cursomentor
— DIVULGUE esta iniciativa!
Até a próxima!
[LSB]
Olá pessoal, estou de volta. Mais uma LIVE realizada, mais um conteúdo disponível.
Agora vamos aos conteúdos de sempre:
O quadro da aula segue abaixo:

Ajude comprando meu ebook:
Para comprar é só CLICAR AQUI E SER FELIZ!
Veja meus outros ebooks:



Por hoje, é só.
Eu sou Leonardo e você veio ao lugar certo pra aprender!
Está é uma iniciativa para trazer materiais de boa qualidade até você e te ajudar a aprender mais.
Vamos crescer mais! Faça parte:
— Doe via PIX: leonardosantos.inf@gmail.com
— Siga-nos nas redes:
Instagram: http://www.instagram.com/mentorblog_oficial
Facebook: https://www.facebook.com/cursomentor
— DIVULGUE esta iniciativa!
Até a próxima!
[LSB]