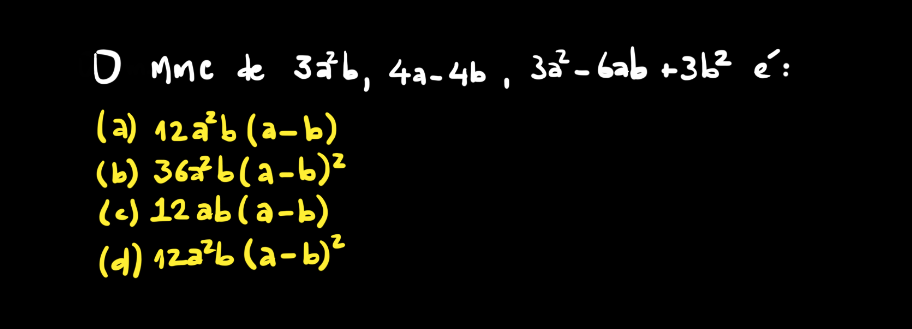O Mínimo Múltiplo Comum (M.M.C.) de Expressões Algébricas: uma Questão da EEAr

Um aluno mandou uma dúvida sobre este assunto que compartilho com vocês agora. Ela trata sobre o MMC de expressões algébricas que caiu na prova da EEAR. Essa é uma questão antiga deste concurso e, atualmente, dificilmente aparecia algo nesse sentido já que o edital se concentra mais em assuntos do ensino médio atualmente.

Apesar disso, este é um assunto muito comum em provas militares (principalmente as que envolvem o conteúdo do 9º ano, tais como CN, EPCAr e Colégios Militares em geral…) e para resolvê-lo, em geral, precisamos única e exclusivamente da definição do que significa o calcular o mínimo múltiplo comum (ou MMC).

A imagem do enunciado da questão segue abaixo.

Como disse, basta aplicar a definição de MMC neste caso. Lembre-se que antes de verificar a solução logo abaixo, seria legal tentar resolver.

Veja que aparece também uma fatoração algébrica envolvendo o quadrado de uma diferença – que é um produto notável. Como falei, trata-se de uma questão simples (o que, via de regra nem sempre é fácil…), no sentido de que, conhecida a definição de MMC, o resto torna-se banal.

Ainda tem dúvida? Mais questões como essa? Conte-nos nos comentários e, até a próxima!

[LSB]

Problema da Semana #9: Solução e a Proposta de um Novo Problema

Estamos de volta para falar do problema da semana #9 e trazer sua solução, bem como os nomes dos que solucionaram e também para fazer algumas considerações gerais.

Relembrando o problema, o enunciado era o seguinte:

(AMAN — 1984) Calcular a soma das raízes da equação:

$2^{x^2} = 32(2^{3x-7})$

a) $3$

b) $2$

c) $-3$

d) $-2$

e) N.R.A.

Como podemos ver, esse é um problema da Academia Militar das Agulhas Negras (AMAN), e envolve uma espécie de equação exponencial. Como a base é $2$ , basta que os expoentes sejam iguais para que a igualdade seja verificada. Então, teremos:

$2^{x^2} = 2^5 \cdot 2^{3x - 7} \Leftrightarrow 2^{x^2} = 2^{5 + 3x - 7}$

Portanto:

$2^{x^2} = 2^{3x - 2} \Leftrightarrow x^2 = 3x - 2 \Leftrightarrow x^2 - 3x + 2 = 0$

Como queremos apenas a soma das raízes e não as raízes em si, basta calcular a soma que vale $S = -\frac{-3}{1} = 3$ . Caso você quisesse achar as raízes bastaria verificar que:

$x^2 - 3x + 2 = 0 \Leftrightarrow (x-1)(x-2) = 0$

Ou seja, as raízes são $x_1 = 1$ e $x_2 = 2$ e, claramente, $x_1 + x_2 = 1+2 = 3$ . Agora deixo para vocês a seguinte pergunta:

Calcular a soma das raízes de: $x^{x^2} = x^5(x^{3x-7})$ .

Isso muda algo? Ou é apenas uma simples troca de base? Pense e me responda nos comentários.

Resolveram este problema:

Lucca Gabriel
Lucas Lopes
Arthur Rocha
@mariopersico_
Ygor Farias
Iuri Henrique
Micael França

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(2) Micael França
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata

Continuem se empenhando e, claro, NUNCA DESISTAM! Estamos juntos e bora para o problema da semana #10.

[LSB]

Teorema do Impulso. Você sabe aplicar?

Um teorema comum utilizado em física básica afirma que o impulso causado por uma força equivale a variação de seu momento linear. A questão a seguir da Mackenzie usa este teorema de forma interessante.

(MACK-SP) Um corpo em repouso e de $1,0$ t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo ( $t$ ) segundo a função $F = 200 t$ , no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante $t = 10$ s vale:

a) $3,6$ km/h.

b) $7,2$ km/h.

c) $36$ km/h.

d) $72$ km/h.

e) $90$ km/h.

O mais importante é perceber que a força, nesse caso é variável, dada por $F(t) = 200t$ , ocasionando o gráfico abaixo:

Assim, precisamos usar a força média, uma vez que o impulso total de uma força é igual a variação da quantidade de movimento (ou do momento linear). Repare que, neste caso, a direção da força é constante, facilitando parcialmente nossa análise.

Assim, teremos:

$\int_0^t \vec{F}\,dt = \Delta \vec{Q}$

Ou seja, a área abaixo do gráfico $F \times t$ é igual à variação de momento linear unidimensional (em uma única direção). Daí, como $F = 200t$ e $t = 10$ s, teremos $F = 2000$ N e, por conta disso:

$\dfrac{10 \times 2000}{2} = m \cdot (v - v_0) \Leftrightarrow \dfrac{10 \times 2000}{2} = 1000 \cdot (v - 0) \Leftrightarrow 1000 = 1000 v$

Ou seja, a velocidade final é de $v = 10$ m/s e, finalmente, passando para km/h teremos $10 \times 3,6 = 36$ km/h. Opção C.

E aí, acertou essa?

Se sim, parabéns; se não, bora para a próxima!

[LSB]

Segmentos e Seus Pontos Médios: Um Bom Desenho Sempre Ajuda!

Olá, hoje trago um problema proposto como dúvida por uma aluna. O problema envolve apenas o conceito de ponto médio de segmentos e as medidas de alguns segmentos adjacentes. O enunciado não traz a figura e, por isso, desenhar uma boa figura já ajuda em boa parte para resolver o problema.

Segue o enunciado abaixo.

Antes de ver a solução, tente resolver sozinho. O conceito de segmento de reta é simples e faz parte do início do estudo da geometria plana. É importante para formular e resolver problemas e ajuda em várias áreas como, por exemplo, trigonometria e/ou geometria analítica.

Se você já tentou resolver e não conseguiu, segue abaixo a solução. Mas é importante tentar, lembre-se que a dúvida é o start importante para a construção do conhecimento.

E aí, acertou?

Mande seus comentários para nós!

[LSB]

Qual a Diferença Entre o Total de Quadrados e o Total de Triângulos?

Neste post trazemos uma das questões de nosso simulado diagnóstico. A pergunta em questão é a número 7. Este tipo de problema aparece muito em provas dos Colégios Militares e em Olimpíadas de Matemática.

O simulado diagnóstico serve essencialmente para entender qual o nível de conhecimento dos alunos que estão conosco. Feito em várias etapas de nossos cursos, este tipo de avaliação traz informações valiosas sobre a bagagem anterior ao próprio curso. Isto nos permite adequar a ementa do curso a realidade do aluno.

Se você quiser ver o arquivo original da prova de matemática, veja a seguir e, caso queira baixa-la, clique no link logo abaixo:

Simulado Diagnóstico de Matemática Baixar

E aí? O que achou das questões? E do nível geral da prova? Tem dúvida em alguma outra questão deste diagnóstico?

E você, por acaso, já tinha visto um problema deste tipo em algum concurso (militar ou não)? Conte-nos nos comentários a seguir e acompanhe-nos por aqui ou no YouTube e nas redes sociais.

Até a próxima!

[LSB]

Um Problema de Desigualdades e Divisibilidade

Segue um problema trazido por um de nossos alunos, cujo enunciado segue na imagem abaixo:

Problemas como esse, que envolvem desigualdades (inequações) e algumas observações sobre o conjunto universo das soluções, bem como a divisibilidade envolvendo as parcelas, são comuns na prova da Escola Naval, por exemplo.

Este, de forma geral não é difícil. Sugerimos que você tente resolver antes de ver a solução. Que segue abaixo. Mas, não perca muito tempo. Caso tenha dificuldade, venha ver a solução.

E aí, conseguiu? Já tinha visto um problema como esse? Conte para nós nos comentários.

Dúvida enviada por Leonardo Lourenço Errera.

Até a próxima.

[LSB]

Problema da Semana #8: Solução e Comentários

Olá, estamos de volta trazendo a solução do problema da semana #8. O problema foi adaptado do livro The Standford Mathematics Problem Book – Hints and Solutions do G. Polya e J. Kilpatrick.

Este é um problema clássico de sistemas de equações que seguem um determinado padrão de repetição. Isto é muito cobrado principalmente pelos concursos do Colégio Naval, Escola Naval, EFOMM que, repare, todos são da Marinha do Brasil (nada é por acaso!). Segue o enunciado:

Encontrar valores $x$ , $y$ , $z$ e $w$ , tais que:

$\left\{ \begin{array}{rcl} x + y + z &=& 4 \\ y + z + w &=& -5 \\ w + z + x &=& 0 \\ w + x + y &=& -8 \end{array}\right.$

E calcule o valor de $x^2 + y^2 + z^2 + w^2$ .

Vamos então falar da solução. Perceba que é possível solucionar isolando cada incógnita até que se tenha apenas uma equação com uma incógnita. Mas isso levaria muito mais tempo. Há um caminho mais simples. Basta somar todas as equações membro a membro e ficamos com:

$3x + 3y + 3z + 3w = -9 \Leftrightarrow x + y + z + w = -3$

Daí, basta perceber, da primeira equação, que $x + y + z = 4$ , portanto $w = -7$ . Na segunda equação $y + z + w = -5$ , logo $x = 2$ . Tendo $w$ e $x$ , na terceira equação teremos $z = 5$ , Finalmente, $2 + y + 5 - 7 = -3 \Leftrightarrow y = -3$ . Então:

$x^2 + y^2 + z^2 + w^2 = 2^2 + (-3)^2 + 5^2 + (-7)^2 = 4+9+25+49 = 87$

Fica então a dica: sistemas nos quais cada equação é semelhante às demais, omitindo apenas uma (ou mais variáveis) de forma similar basta verificar se é possível adicionar (ou multiplicar) as equações e obter um “atalho”.

Resolveram este problema:

Alef
Gustavo
Arthur Rocha
@mariopersico_
Ygor Farias
Iuri Henrique
Davi do Nascimento Teles Barata
Micael França
Ygor Gabriel

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(2) Yasmim Silva
(2) Ygor Farias
(1) Arthur Rocha
(1) Alef
(1) Iuri Henrique
(1) Gustavo
(1) @mariopersico_
(1) Davi do Nascimento Teles Barata
(1) Micael França

Vamos pra cima, em breve, o problema da próxima semana. Continuem estudando, até mais.
[LSB]

LIVE: UERJ (Física) e Outros

Alguns Links úteis:

Livro Física na EEAr — Volume 2: AQUI
Grupo do WhatsApp (MAT/FIS): AQUI
Perfil do Instagram: AQUI

Eu sou Leonardo Santos e você veio ao lugar certo pra aprender!

Está é uma iniciativa para trazer materiais de boa qualidade até você e te ajudar a aprender mais.

Vamos crescer mais! Faça parte:

— Doe via PIX: leonardosantos.inf@gmail.com

— Siga-nos nas redes:

Instagram: http://www.instagram.com/mentorblog_oficial

Facebook: https://www.facebook.com/cursomentor

— DIVULGUE esta iniciativa!

Até a próxima!

[LSB]

LIVE: UERJ 2022 Matemática e Outros

Olá leitores, estamos de volta com mais uma LIVE. Nesta, trazemos todas as questões da UERJ integralmente resolvidas para vocês. Vamos aos links da semana:

Compre meu ebook “Física na EEAr — Volume 2”: É SÓ R$ 9,90 CLICA AQUI E COMPRA!
Entre em nosso grupo do Whatsapp para receber as listas semanalmente: CLICA AQUI E ENTRA AGORA!
Acesse nosso instagram: VAI LÁ AGORA!
Lista desta LIVE: CLICA AQUI E PEGA A LISTA!

Abaixo você tem o “quadro” com as soluções das questões da LIVE: