Na última postagem falamos sobre um problema cuja solução envolvia o impulso e a quantidade de movimento (ou momento linear). Mas será que há outra solução? E a resposta é: sim! Há outra solução. Mas antes vamos relembrar qual o enunciado. Segue:
(MACK-SP) Um corpo em repouso e de
t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo (
) segundo a função
, no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante
s vale:
a)
km/h.
b)
km/h.
c)
km/h.
d)
km/h.
e)
km/h.
Vamos fazer o seguinte: primeiro vamos encontrar o formato da aceleração em função do tempo, que neste caso, obviamente, não será constante:
Como kg, teremos
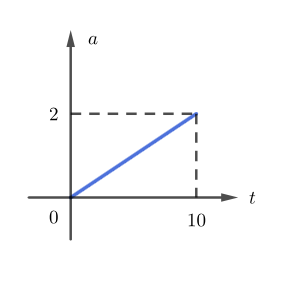
(S.I.), cujo gráfico segue na imagem a seguir.
Agora vem uma parte importante: como a área entre o gráfico de
em função do tempo e o eixo horizontal representa a variação de velocidade. Em outras palavras, se
, então
e:
Que representa a variação de velocidade entre os instantes e
. Assim, a área será de
m/s ou
km/h. Veja que na integral teríamos o mesmo:
m/s
Assim, é possível termos o mesmo valor final usando tanto a integral quanto apenas a área abaixo da curva .
Esta solução foi proposta por Diego Gorito, com algumas adaptações minhas para incluir a parte de cálculo e atende ao Matheus Teixeira que queria uma solução que não envolvesse o impulso.
Até próxima pessoal!
[LSB]