Segue um problema de geometria plana; simples, mas interessante.
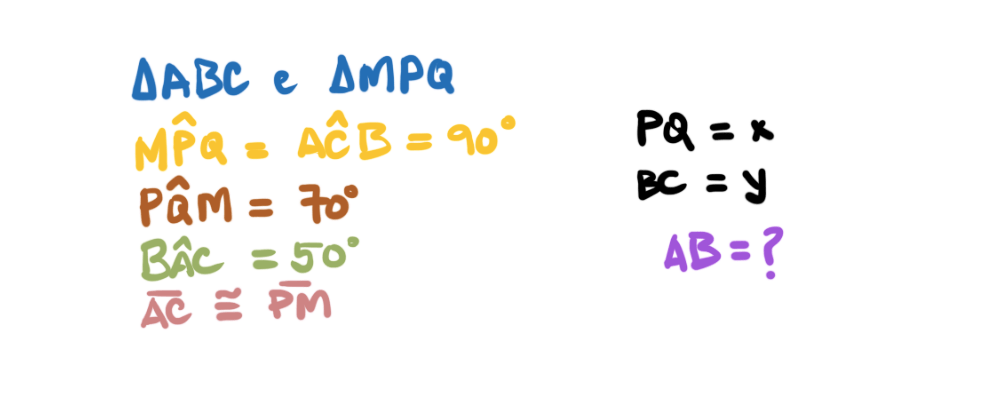
Quesemos encontrar o valor de . A solução segue abaixo:
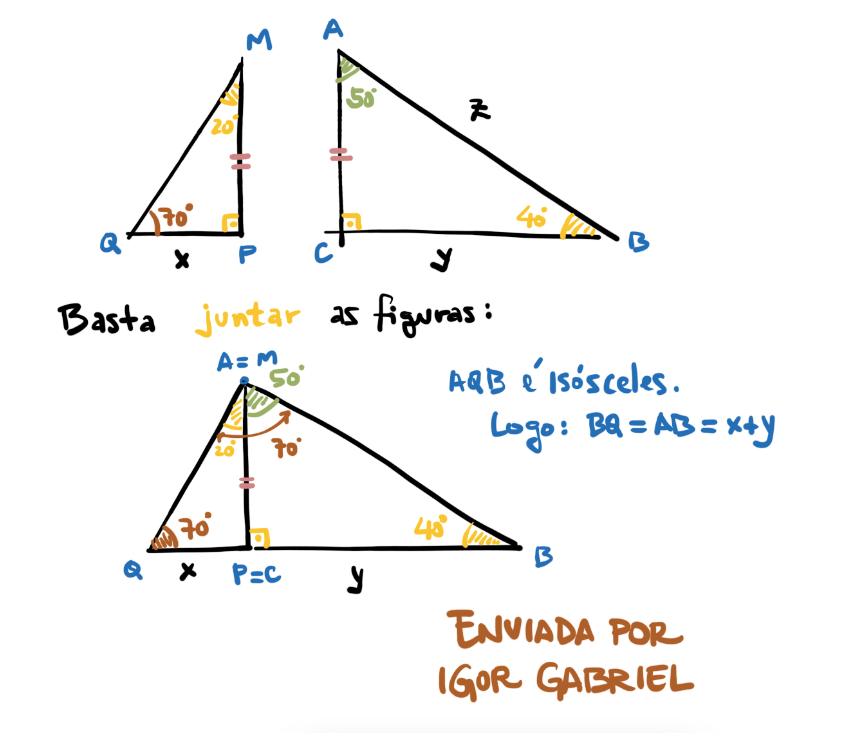
Até a próxima dúvida e boa semana!












Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
Segue um problema de geometria plana; simples, mas interessante.
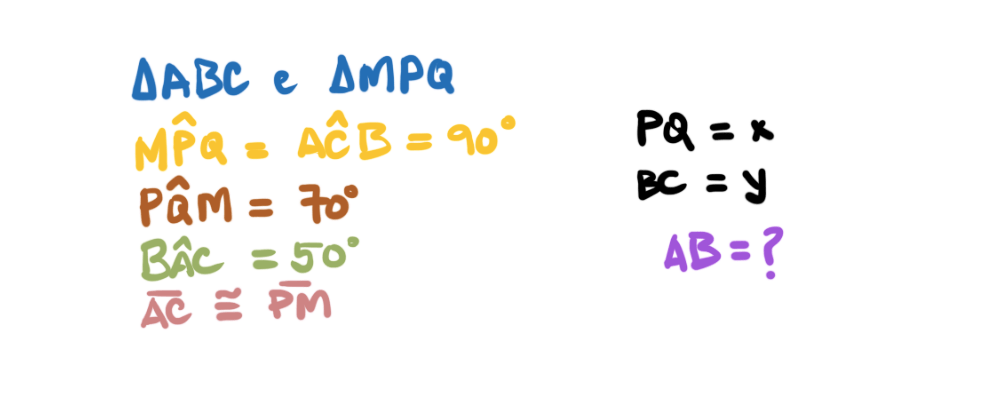
Quesemos encontrar o valor de . A solução segue abaixo:

Até a próxima dúvida e boa semana!













Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
Olá, estamos de volta trazendo a solução do problema da semana #8. O problema foi adaptado do livro The Standford Mathematics Problem Book – Hints and Solutions do G. Polya e J. Kilpatrick.
Este é um problema clássico de sistemas de equações que seguem um determinado padrão de repetição. Isto é muito cobrado principalmente pelos concursos do Colégio Naval, Escola Naval, EFOMM que, repare, todos são da Marinha do Brasil (nada é por acaso!). Segue o enunciado:
Encontrar valores
,
,
e
, tais que:
E calcule o valor de
.
Vamos então falar da solução. Perceba que é possível solucionar isolando cada incógnita até que se tenha apenas uma equação com uma incógnita. Mas isso levaria muito mais tempo. Há um caminho mais simples. Basta somar todas as equações membro a membro e ficamos com:
Daí, basta perceber, da primeira equação, que , portanto
. Na segunda equação
, logo
. Tendo
e
, na terceira equação teremos
, Finalmente,
. Então:
Fica então a dica: sistemas nos quais cada equação é semelhante às demais, omitindo apenas uma (ou mais variáveis) de forma similar basta verificar se é possível adicionar (ou multiplicar) as equações e obter um “atalho”.
Resolveram este problema:
Listagem de problemas resolvidos até agora:
Vamos pra cima, em breve, o problema da próxima semana. Continuem estudando, até mais.
[LSB]
Questão enviada por Ederson Ferreira
(CONED-CASTANHAL 2009-PA) João, Pedro e Marcos são amigos e trabalham juntos. Sabe-se que João e Pedro trabalham juntos constroem um muro em dias. Trabalhando juntos João e Marcos levam
dias para construir o mesmo muro. Pedro e Marcos, juntos levam
dias para construir o mesmo muro. Podemos afirmar que Marcos trabalhando sozinho, levará para fazer o mesmo muro:
a) dias
b) dias
c) dias
d) dias
e) dias
Veja a solução aqui.