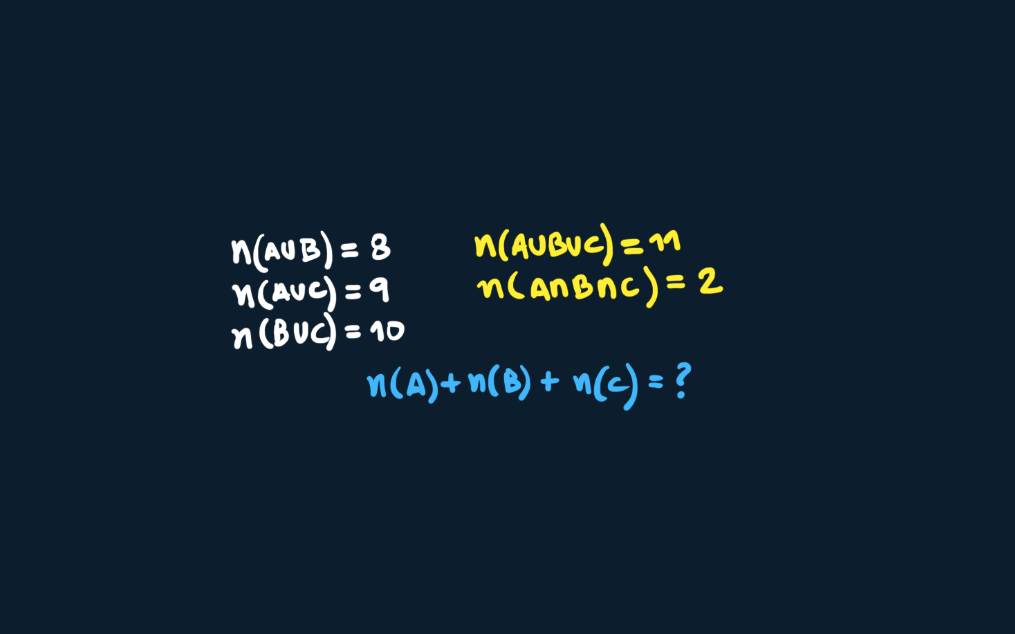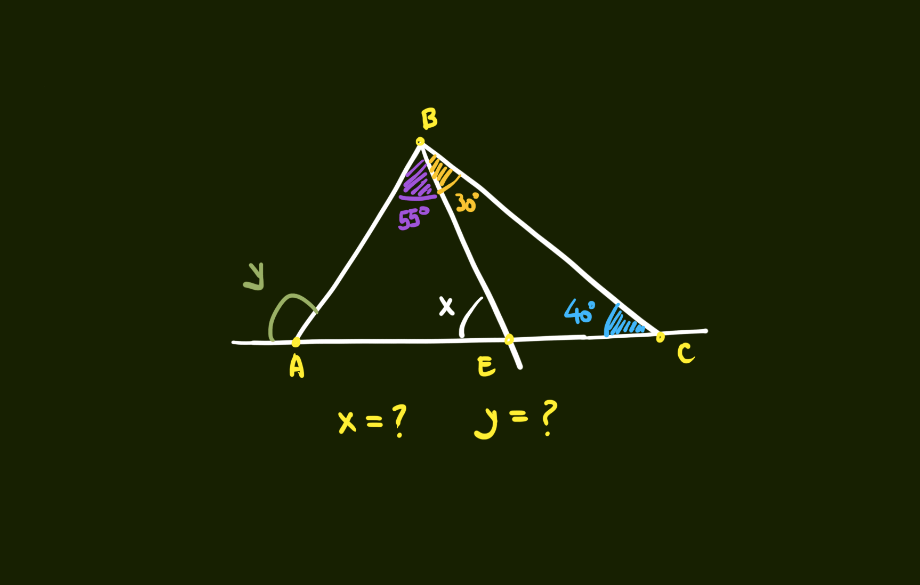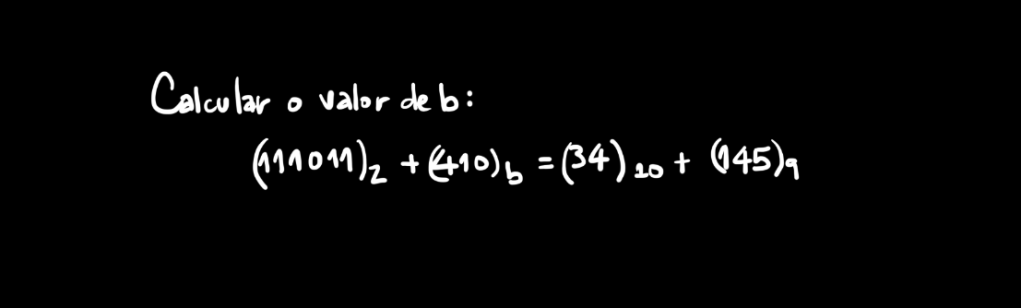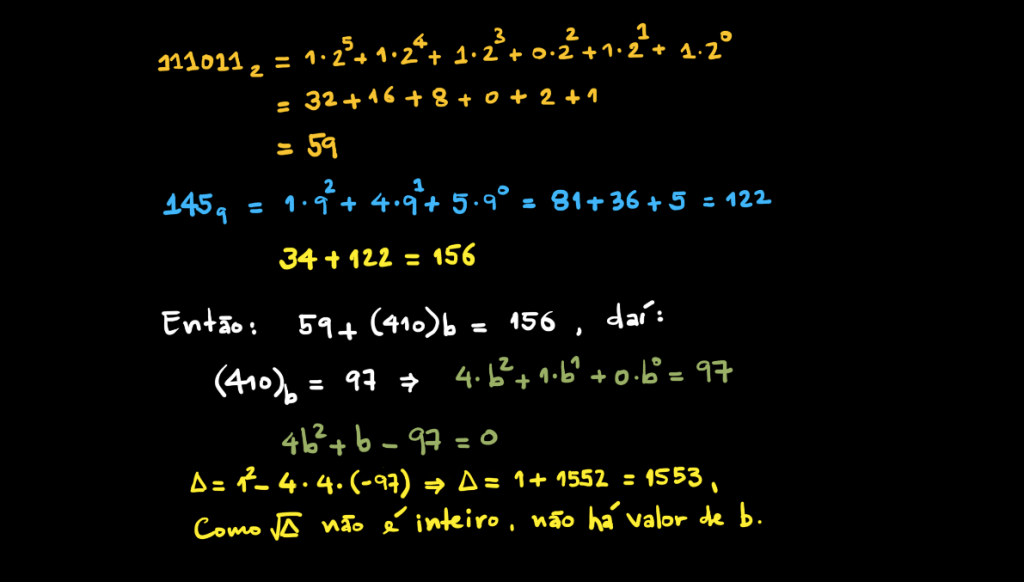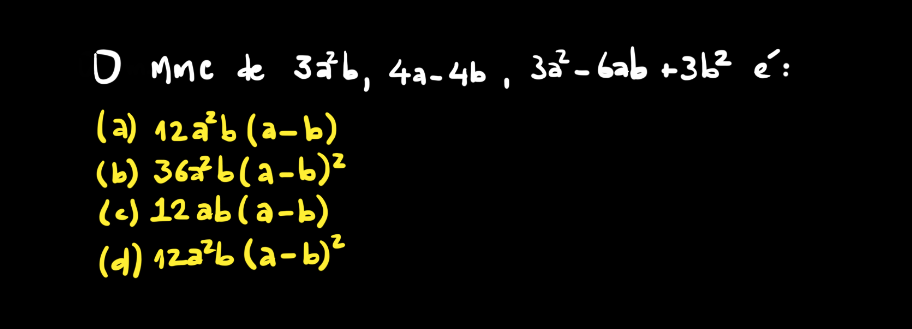Tira-Teima #2

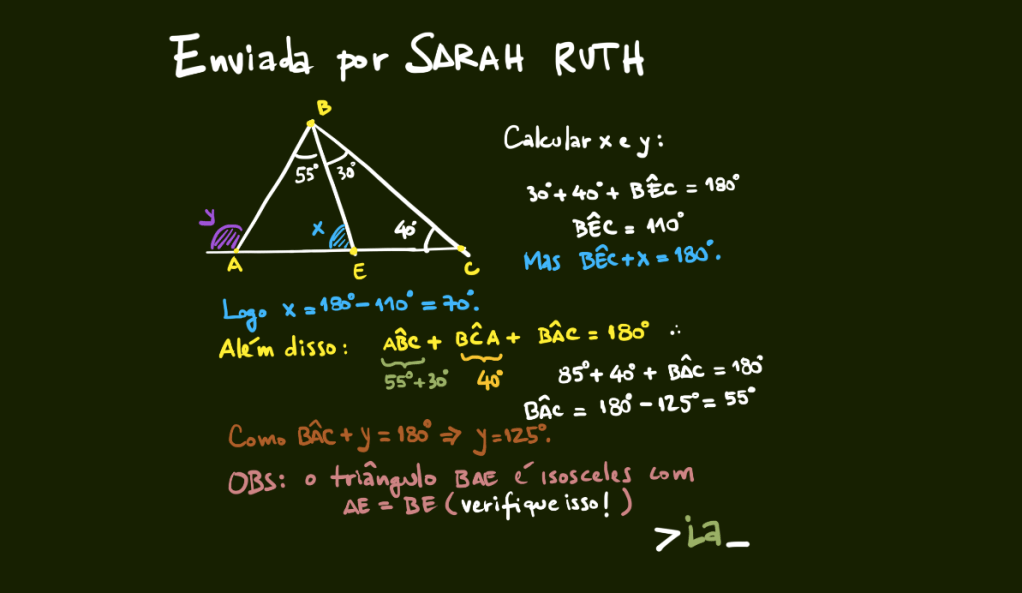
Tira-Teima #1

Existe o Valor de b?

Estamos de volta com mais uma dúvida enviada para nós.

O problema em questão trata de sistemas de numeração. Neste caso, além da base $10$ há outras bases envolvidas.

A solução segue na imagem abaixo:

Veja que não é possível, uma vez que $b$ não será um número inteiro.

Até a próxima.

[LSB]

Problema da Semana #10: Uma Solução Mais ou Menos Simples

Segue a solução do problema da semana #10. Vamos relembrar o enunciado.

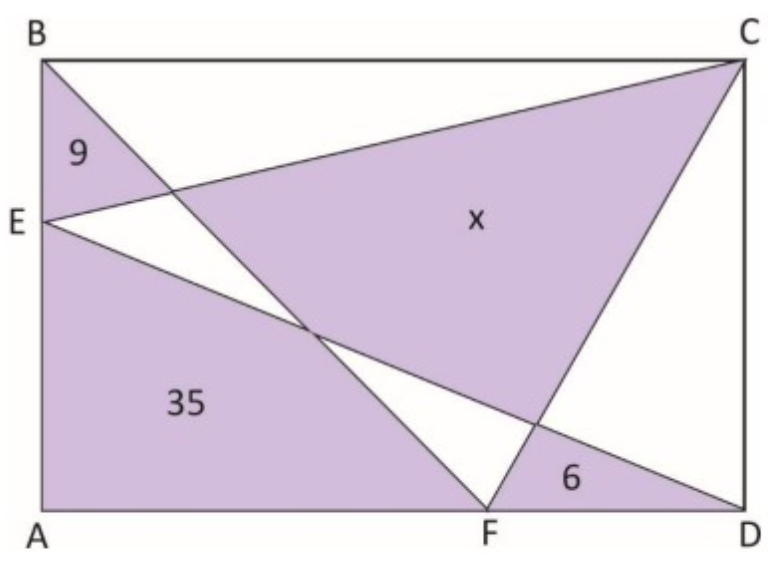
Na figura abaixo, o terreno retangular $ABCD$ foi loteado e os números que aparecem no interior de alguns destes lotes, indicam suas respectivas áreas em $\text{km}^2$ .

A medida da área indicada pelo lote da letra $x$ , em $\text{km}^2$ é igual a:

a) $70$

b) $40$

c) $60$

d) $50$

e) $54$

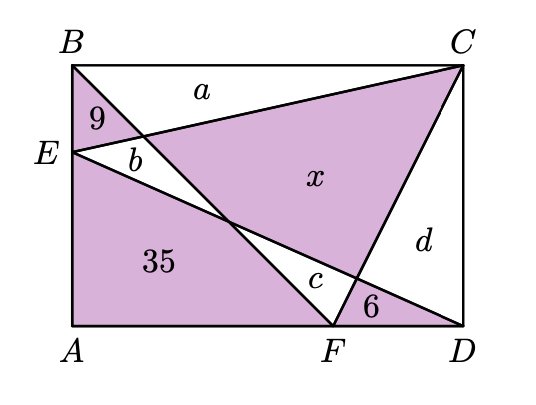
Uma solução “simples” é chamar a áreas desconhecidas em branco de $a$ , $b$ , $c$ e $d$ . Como na figura abaixo:

Perceba que a área do triângulo $BCF$ é igual à área do triângulo $CDE$ , pois ambos são iguais a metade da área do retângulo (esse pode ser um fato difícil de perceber, pense um pouco até que isso fique claro para você). Assim, podemos escrever:

$a+x + c = b + x + d \Leftrightarrow a+c = b+d$

Pelo mesmo motivo teremos:

$9 + b + 35 + 6 + d = a + x + c \Leftrightarrow 50 + \underbrace{b + d}_{= a+c} = x + a + c$

Logo $x = 50$ . Há outra solução usando o Teorema dos Carpetes. Mas essa deixaremos para o grande mentor José Maria Gomes (o famoso China).

Resolveram este Problema:

Micael França

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(3) Micael França
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata
(1) Enzo Botarelli

Se seu nome não apareceu, me avise pois pode ser que eu não tenha visto a sua solução enviada.

Bora pra cima!

O Mínimo Múltiplo Comum (M.M.C.) de Expressões Algébricas: uma Questão da EEAr

Um aluno mandou uma dúvida sobre este assunto que compartilho com vocês agora. Ela trata sobre o MMC de expressões algébricas que caiu na prova da EEAR. Essa é uma questão antiga deste concurso e, atualmente, dificilmente aparecia algo nesse sentido já que o edital se concentra mais em assuntos do ensino médio atualmente.

Apesar disso, este é um assunto muito comum em provas militares (principalmente as que envolvem o conteúdo do 9º ano, tais como CN, EPCAr e Colégios Militares em geral…) e para resolvê-lo, em geral, precisamos única e exclusivamente da definição do que significa o calcular o mínimo múltiplo comum (ou MMC).

A imagem do enunciado da questão segue abaixo.

Como disse, basta aplicar a definição de MMC neste caso. Lembre-se que antes de verificar a solução logo abaixo, seria legal tentar resolver.

Veja que aparece também uma fatoração algébrica envolvendo o quadrado de uma diferença – que é um produto notável. Como falei, trata-se de uma questão simples (o que, via de regra nem sempre é fácil…), no sentido de que, conhecida a definição de MMC, o resto torna-se banal.

Ainda tem dúvida? Mais questões como essa? Conte-nos nos comentários e, até a próxima!

[LSB]

Problema da Semana #9: Solução e a Proposta de um Novo Problema

Estamos de volta para falar do problema da semana #9 e trazer sua solução, bem como os nomes dos que solucionaram e também para fazer algumas considerações gerais.

Relembrando o problema, o enunciado era o seguinte:

(AMAN — 1984) Calcular a soma das raízes da equação:

$2^{x^2} = 32(2^{3x-7})$

a) $3$

b) $2$

c) $-3$

d) $-2$

e) N.R.A.

Como podemos ver, esse é um problema da Academia Militar das Agulhas Negras (AMAN), e envolve uma espécie de equação exponencial. Como a base é $2$ , basta que os expoentes sejam iguais para que a igualdade seja verificada. Então, teremos:

$2^{x^2} = 2^5 \cdot 2^{3x - 7} \Leftrightarrow 2^{x^2} = 2^{5 + 3x - 7}$

Portanto:

$2^{x^2} = 2^{3x - 2} \Leftrightarrow x^2 = 3x - 2 \Leftrightarrow x^2 - 3x + 2 = 0$

Como queremos apenas a soma das raízes e não as raízes em si, basta calcular a soma que vale $S = -\frac{-3}{1} = 3$ . Caso você quisesse achar as raízes bastaria verificar que:

$x^2 - 3x + 2 = 0 \Leftrightarrow (x-1)(x-2) = 0$

Ou seja, as raízes são $x_1 = 1$ e $x_2 = 2$ e, claramente, $x_1 + x_2 = 1+2 = 3$ . Agora deixo para vocês a seguinte pergunta:

Calcular a soma das raízes de: $x^{x^2} = x^5(x^{3x-7})$ .

Isso muda algo? Ou é apenas uma simples troca de base? Pense e me responda nos comentários.

Resolveram este problema:

Lucca Gabriel
Lucas Lopes
Arthur Rocha
@mariopersico_
Ygor Farias
Iuri Henrique
Micael França

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(2) Micael França
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata

Continuem se empenhando e, claro, NUNCA DESISTAM! Estamos juntos e bora para o problema da semana #10.

[LSB]

Uma Nova Solução, para um Problema Antigo!

Na última postagem falamos sobre um problema cuja solução envolvia o impulso e a quantidade de movimento (ou momento linear). Mas será que há outra solução? E a resposta é: sim! Há outra solução. Mas antes vamos relembrar qual o enunciado. Segue:

(MACK-SP) Um corpo em repouso e de $1,0$ t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo ( $t$ ) segundo a função $F = 200 t$ , no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante $t = 10$ s vale:

a) $3,6$ km/h.

b) $7,2$ km/h.

c) $36$ km/h.

d) $72$ km/h.

e) $90$ km/h.

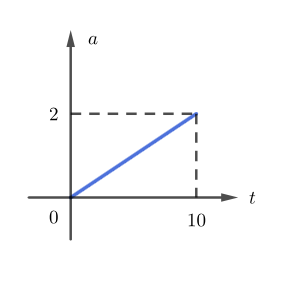
Vamos fazer o seguinte: primeiro vamos encontrar o formato da aceleração em função do tempo, que neste caso, obviamente, não será constante:

$\vec{F} = m\vec{a} \Leftrightarrow 200 t = m \cdot a$

Como $m = 1000$ kg, teremos $a = 0,2t$ (S.I.), cujo gráfico segue na imagem a seguir.

Agora vem uma parte importante: como $a = \dfrac{\Delta v}{\Delta t}$ a área entre o gráfico de $a$ em função do tempo e o eixo horizontal representa a variação de velocidade. Em outras palavras, se $a = \dfrac{dv}{dt}$ , então $dv = a \, dt$ e:

$\int_0^t dv = \int_0^t a dt \Leftrightarrow v = \int_0^t a\, dt \Leftrightarrow v = \int_0^t 0,2t\, dt$

Que representa a variação de velocidade entre os instantes $0$ e $t$ . Assim, a área será de $\dfrac{10 \times 2}{2} = 10$ m/s ou $36$ km/h. Veja que na integral teríamos o mesmo:

$v = \int_0^t 0,2t\, dt = 0,2\left.\frac{t^2}{2}\right \vert_0^{10} = 0,1 \cdot (10^2 - 0^2) = 10$ m/s

Assim, é possível termos o mesmo valor final usando tanto a integral quanto apenas a área abaixo da curva $a \times t$ .

Esta solução foi proposta por Diego Gorito, com algumas adaptações minhas para incluir a parte de cálculo e atende ao Matheus Teixeira que queria uma solução que não envolvesse o impulso.

Até próxima pessoal!

[LSB]

Teorema do Impulso. Você sabe aplicar?

Um teorema comum utilizado em física básica afirma que o impulso causado por uma força equivale a variação de seu momento linear. A questão a seguir da Mackenzie usa este teorema de forma interessante.

(MACK-SP) Um corpo em repouso e de $1,0$ t de massa é submetido a uma resultante de forças, com direção constante, cuja intensidade varia em função do tempo ( $t$ ) segundo a função $F = 200 t$ , no sistema MKS, a partir do instante zero. A velocidade escalar desse corpo no instante $t = 10$ s vale:

a) $3,6$ km/h.

b) $7,2$ km/h.

c) $36$ km/h.

d) $72$ km/h.

e) $90$ km/h.

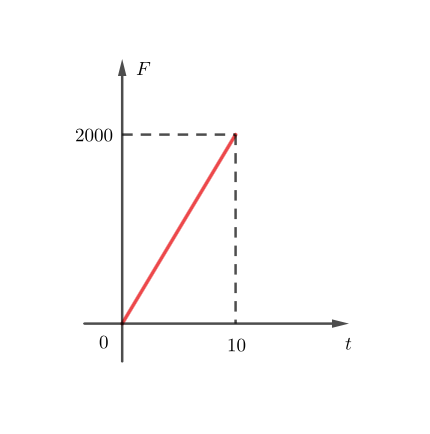
O mais importante é perceber que a força, nesse caso é variável, dada por $F(t) = 200t$ , ocasionando o gráfico abaixo:

Assim, precisamos usar a força média, uma vez que o impulso total de uma força é igual a variação da quantidade de movimento (ou do momento linear). Repare que, neste caso, a direção da força é constante, facilitando parcialmente nossa análise.

Assim, teremos:

$\int_0^t \vec{F}\,dt = \Delta \vec{Q}$

Ou seja, a área abaixo do gráfico $F \times t$ é igual à variação de momento linear unidimensional (em uma única direção). Daí, como $F = 200t$ e $t = 10$ s, teremos $F = 2000$ N e, por conta disso:

$\dfrac{10 \times 2000}{2} = m \cdot (v - v_0) \Leftrightarrow \dfrac{10 \times 2000}{2} = 1000 \cdot (v - 0) \Leftrightarrow 1000 = 1000 v$

Ou seja, a velocidade final é de $v = 10$ m/s e, finalmente, passando para km/h teremos $10 \times 3,6 = 36$ km/h. Opção C.

E aí, acertou essa?

Se sim, parabéns; se não, bora para a próxima!

[LSB]

Vamos Racionalizar a Série a Seguir… “Vai que…”

Sejam bem vindos! Hoje trazemos uma interessante questão sobre radiciação proposta pelo grande mestre Losano em uma de suas avaliações:

Calcule o valor da expressão numérica $\dfrac{1}{\sqrt{6} + \sqrt{5}} + \dfrac{1}{\sqrt{5} + 2} + \dfrac{1}{2 - \sqrt{3}} + \dfrac{1}{\sqrt{3} + \sqrt{2}} + \dfrac{1}{\sqrt{2} - 1}$ .

Sabe fazer? Bem, vale a pena tentar… Se já tentou (~~ou nem quer tentar~~), vamos lá. Vejamos uma solução que não seja sair calculando o mínimo múltiplo comum de todos os denominadores.

A ideia deste problema é a racionalização de denominadores, o que vai gerar uma espécie de série telescópica (se não sabe o que é isso, sem problema!). Assim, vamos racionalizar o denominador de cada parcela, ficando com:

$\frac{1}{\sqrt{6} + \sqrt{5}} \cdot \frac{\sqrt{6} - \sqrt{5}}{\sqrt{6} - \sqrt{5}} + \frac{1}{\sqrt{5} + 2} \cdot \frac{\sqrt{5} - 2}{\sqrt{5} - 2} + \frac{1}{2 - \sqrt{3}} \cdot \frac{2 + \sqrt{3}}{2 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{2}} \cdot \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} + \frac{1}{\sqrt{2} - 1} \cdot \frac{\sqrt{2} + 1}{\sqrt{2} + 1}$

Agora lembre-se que $(a+b)(a-b) = a^2 - b^2$ e aplique isso em cada parcela da soma anterior para cada denominador. Teremos:

$\dfrac{\sqrt{6} - \sqrt{5}}{(\sqrt{6})^2 - (\sqrt{5})^2} + \dfrac{\sqrt{5} - 2}{(\sqrt{5})^2 - 2^2} + \dfrac{2 + \sqrt{3}}{2^2 - (\sqrt{3})^2} + \dfrac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} + \dfrac{\sqrt{2} + 1}{(\sqrt{2})^2 - 1^2}$

Agora, desenvolvendo cada denominador:

$\dfrac{\sqrt{6} - \sqrt{5}}{6-5} + \dfrac{\sqrt{5} - 2}{5-4} + \dfrac{2 + \sqrt{3}}{4-3} + \dfrac{\sqrt{3} - \sqrt{2}}{3-2} + \dfrac{\sqrt{2} + 1}{2 - 1}$

A partir disso:

$\sqrt{6} - \sqrt{5} + \sqrt{5} - 2 + 2 + \sqrt{3} + \sqrt{3} - \sqrt{2} + \sqrt{2} + 1$

Simplificando os termos semelhantes, teremos: $\sqrt{6} + 2\sqrt{3} + 1$

Ufa! Agoooooora… como acreditamos que ela poderia ser, para ficar elegante:

Calcule o valor da expressão numérica $\dfrac{1}{\sqrt{6} + \sqrt{5}} + \dfrac{1}{\sqrt{5} + 2} + \dfrac{1}{2 + \sqrt{3}} + \dfrac{1}{\sqrt{3} + \sqrt{2}} + \dfrac{1}{\sqrt{2} + 1}$ .

Assim, teríamos, ja parte da racionalização dos denominadores:

$\dfrac{\sqrt{6} - \sqrt{5}}{(\sqrt{6})^2 - (\sqrt{5})^2} + \dfrac{\sqrt{5} - 2}{(\sqrt{5})^2 - 2^2} + \dfrac{2 - \sqrt{3}}{2^2 - (\sqrt{3})^2} + \dfrac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} + \dfrac{\sqrt{2} - 1}{(\sqrt{2})^2 - 1^2}$

Ou seja, mais uma vez, todos os denominadores seriam iguais a $1$ e:

$\sqrt{6} - \sqrt{5} + \sqrt{5} - 2 + 2 - \sqrt{3} + \sqrt{3} - \sqrt{2} + \sqrt{2} - 1 = \sqrt{6} - 1$

Portanto, muito (ou não…) mais elegante (modéstia a parte, claro!).

Tmj, mestre Losano.

Até próxima galera!

[LSB]

Segmentos e Seus Pontos Médios: Um Bom Desenho Sempre Ajuda!

Olá, hoje trago um problema proposto como dúvida por uma aluna. O problema envolve apenas o conceito de ponto médio de segmentos e as medidas de alguns segmentos adjacentes. O enunciado não traz a figura e, por isso, desenhar uma boa figura já ajuda em boa parte para resolver o problema.

Segue o enunciado abaixo.

Antes de ver a solução, tente resolver sozinho. O conceito de segmento de reta é simples e faz parte do início do estudo da geometria plana. É importante para formular e resolver problemas e ajuda em várias áreas como, por exemplo, trigonometria e/ou geometria analítica.

Se você já tentou resolver e não conseguiu, segue abaixo a solução. Mas é importante tentar, lembre-se que a dúvida é o start importante para a construção do conhecimento.