Segue a dúvida de um de nossos alunos a respeito de sistemas de bases de numeração. O assunto costuma ser cobrado no Colégio Naval e na EPCAr além de outras provas (concursos) e, justamente por isso, vamos comentar a solução deste problema aqui. Eis a pergunta:
O número  corresponde na base
corresponde na base 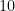 a:
a:
a) 
b) 
c) 
d) 
e) 
Como sabemos, para passar da base  para a base
para a base 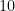 só precisamos “expandir” o número na base dada e realizar os cálculos na base
só precisamos “expandir” o número na base dada e realizar os cálculos na base 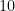 . Então, para o número dado, teríamos:
. Então, para o número dado, teríamos:

Veja que a parte decimal começa a ter os expoentes inteiros negativos, seguindo a partir do zero que é o expoente da base correspondente à ordem das unidades. Então, desenvolvendo:

Como  , teremos
, teremos  , ou seja, opção C.
, ou seja, opção C.
Entendeu? Então tente converter, por exemplo,  para a base
para a base 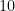 e me conte o que encontrou nos comentários abaixo.
e me conte o que encontrou nos comentários abaixo.
Um grande abraço e nos vemos por aí.
[LSB]
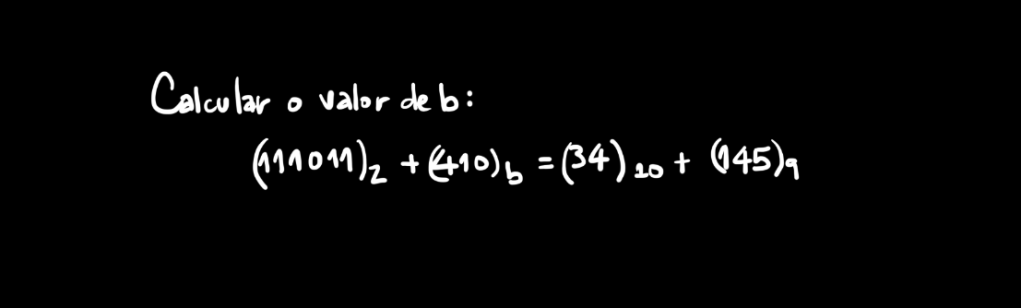
há outras bases envolvidas.
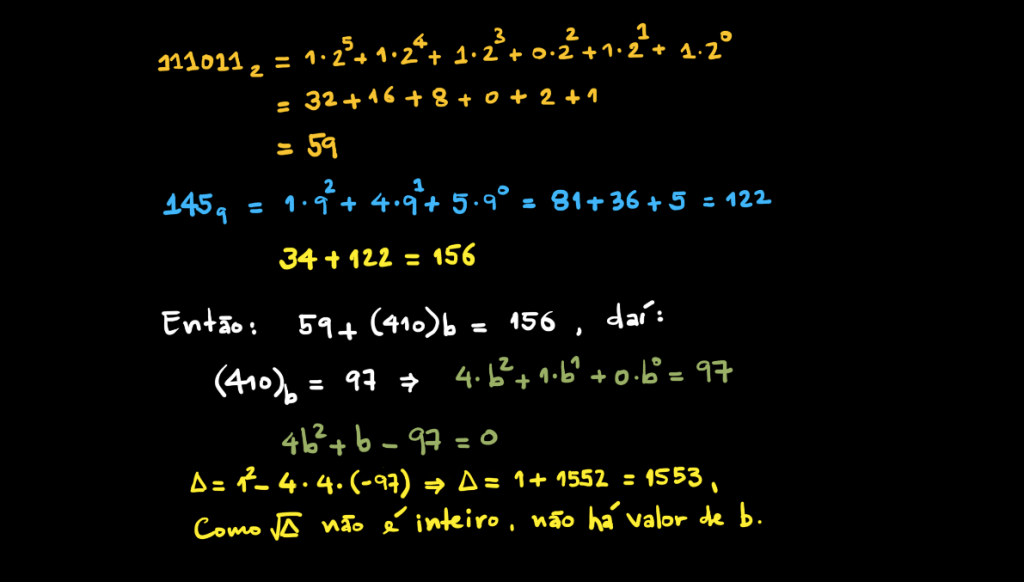
não será um número inteiro.



