Segue mais uma dúvida de nossos alunos:
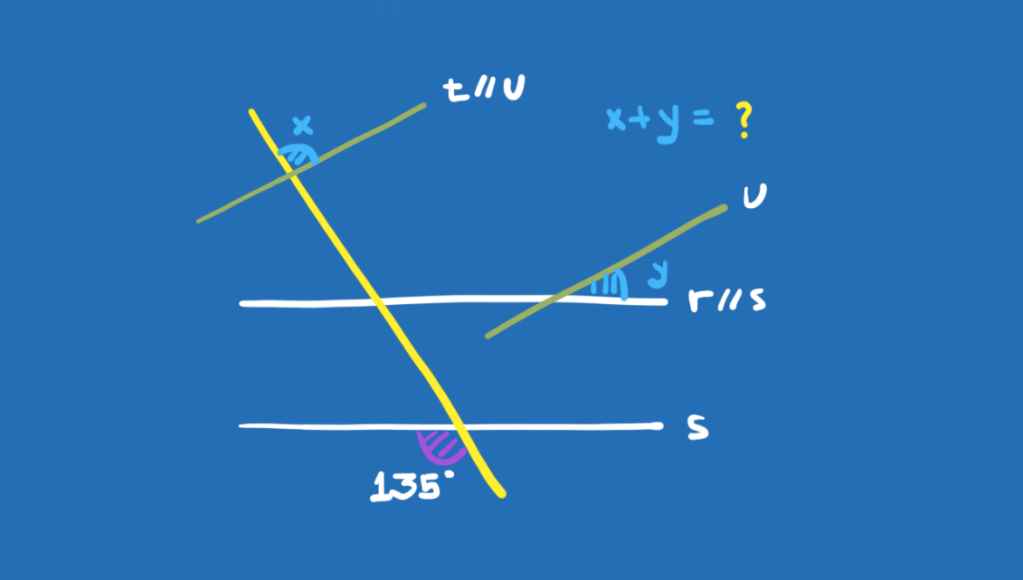
Cuja solução segue abaixo:
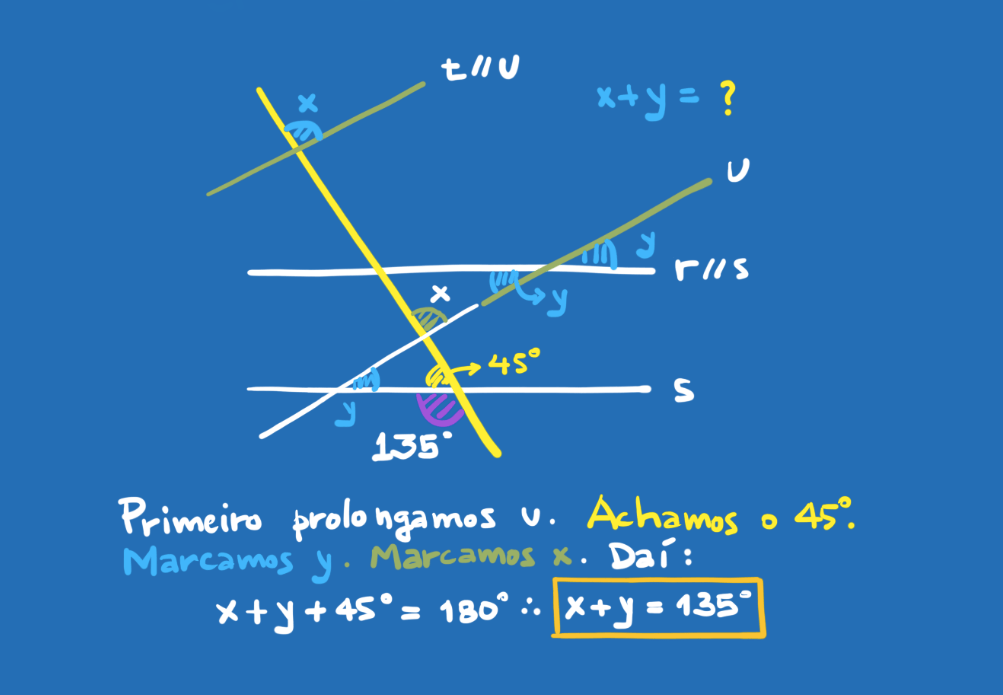
Nossa loja de camisetas: http://reserva.ink/equilateral
Segue mais uma dúvida de nossos alunos:
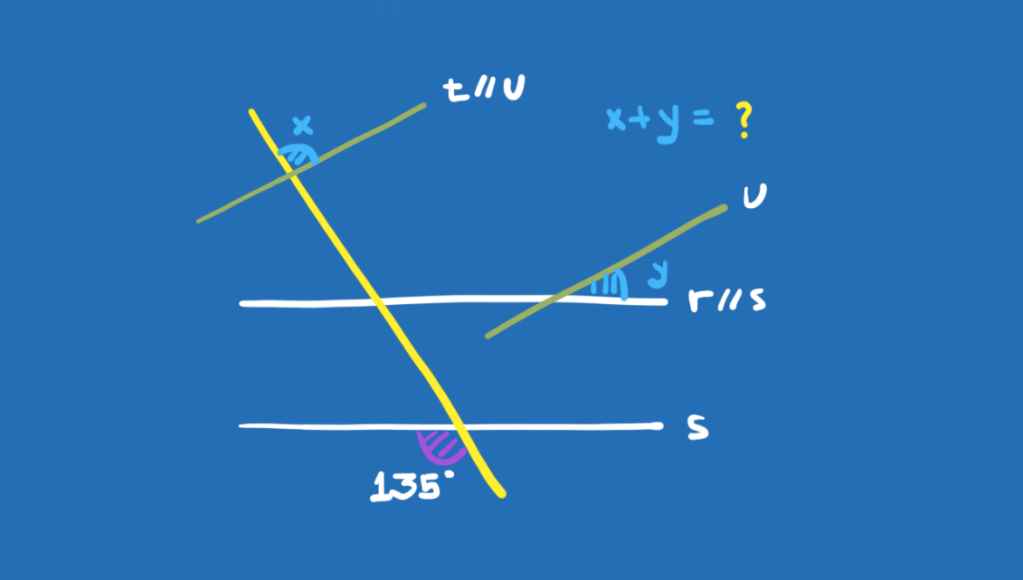
Cuja solução segue abaixo:
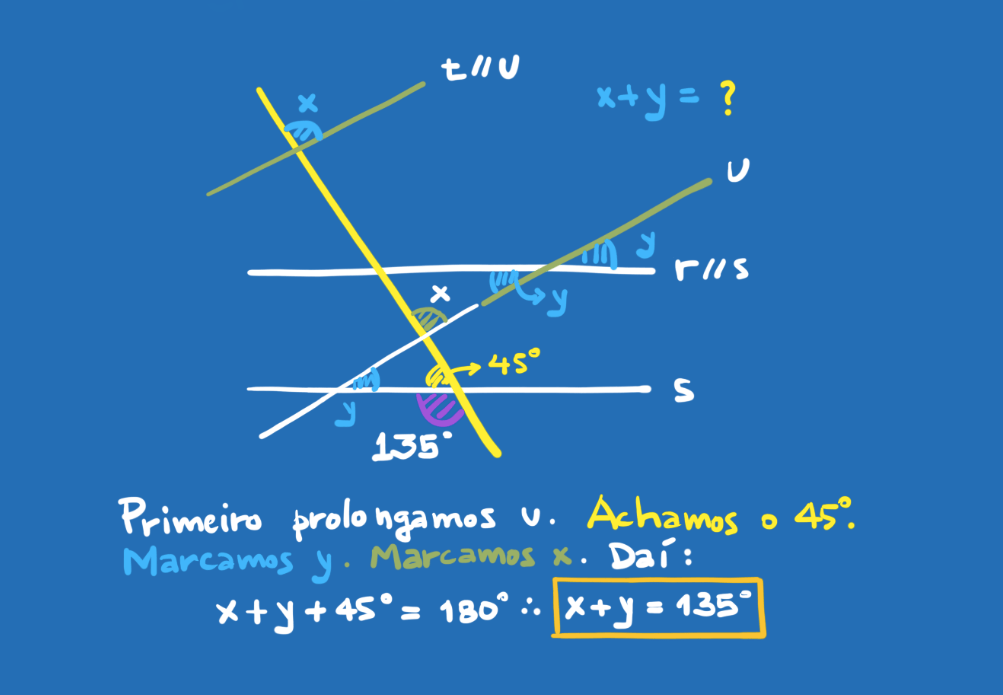
Nossa loja de camisetas: http://reserva.ink/equilateral
Segue um problema de geometria plana; simples, mas interessante.
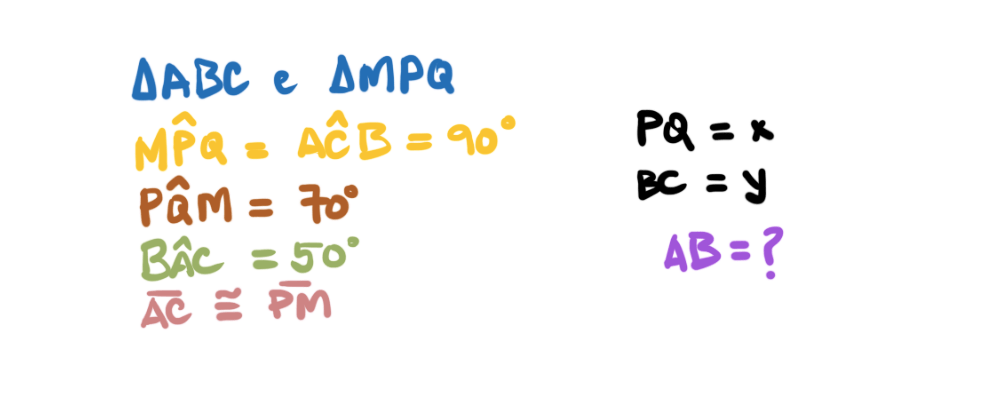
Quesemos encontrar o valor de . A solução segue abaixo:
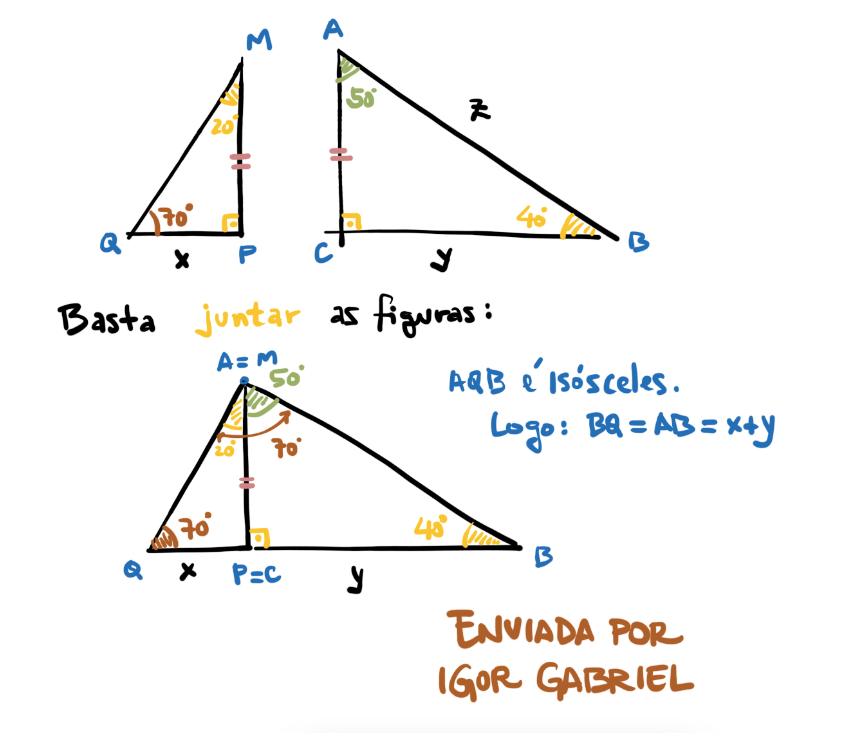
Até a próxima dúvida e boa semana!






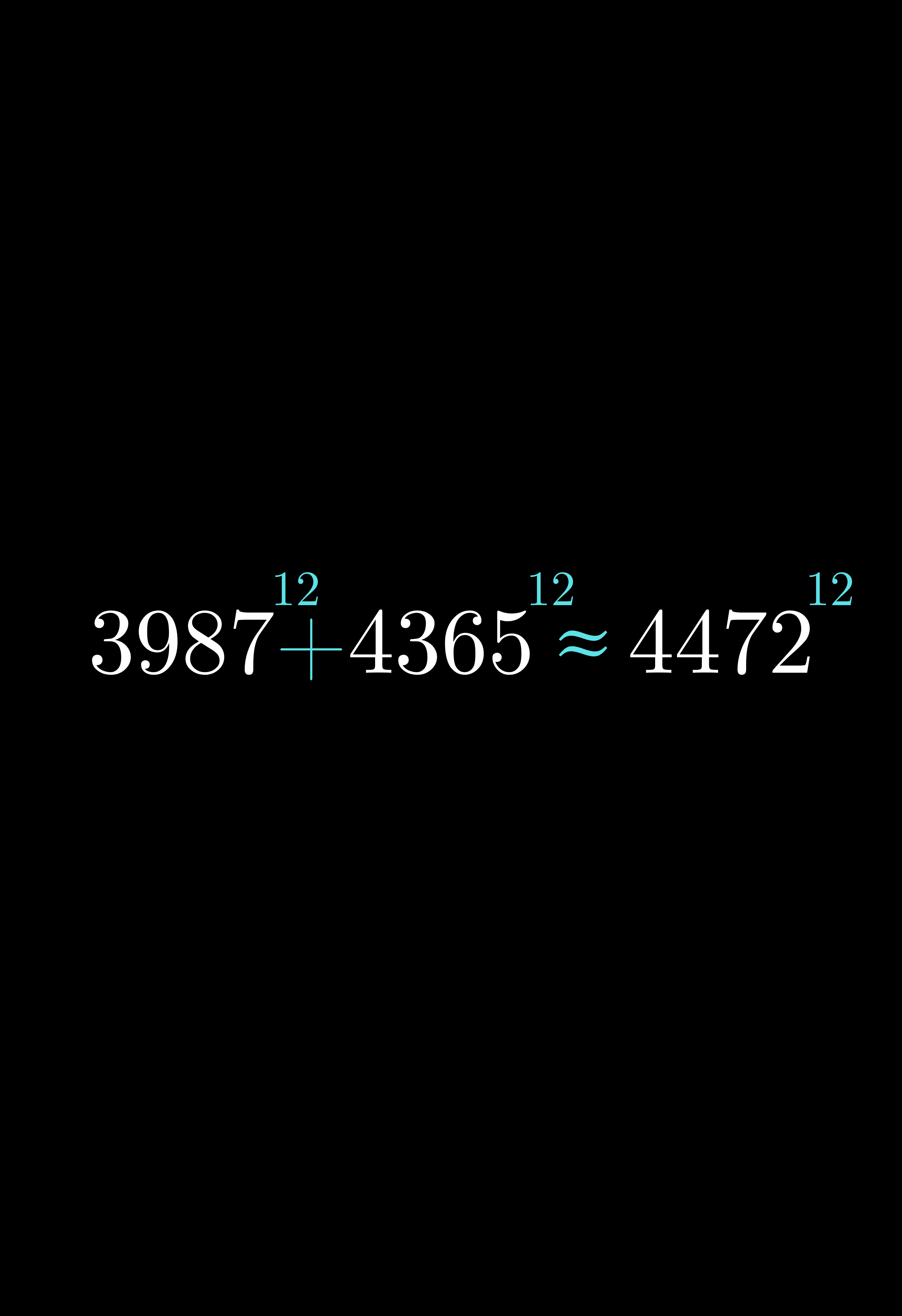



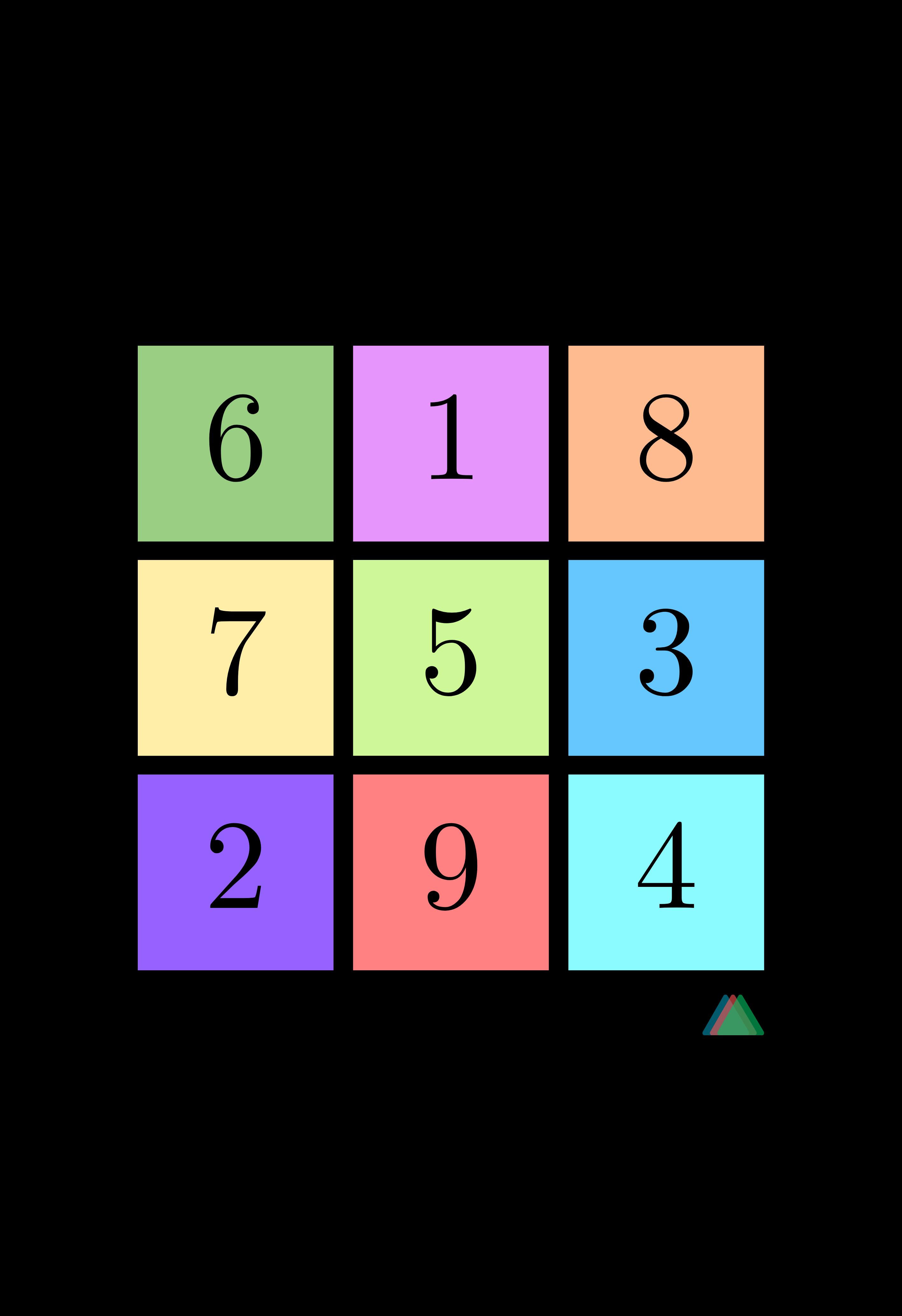

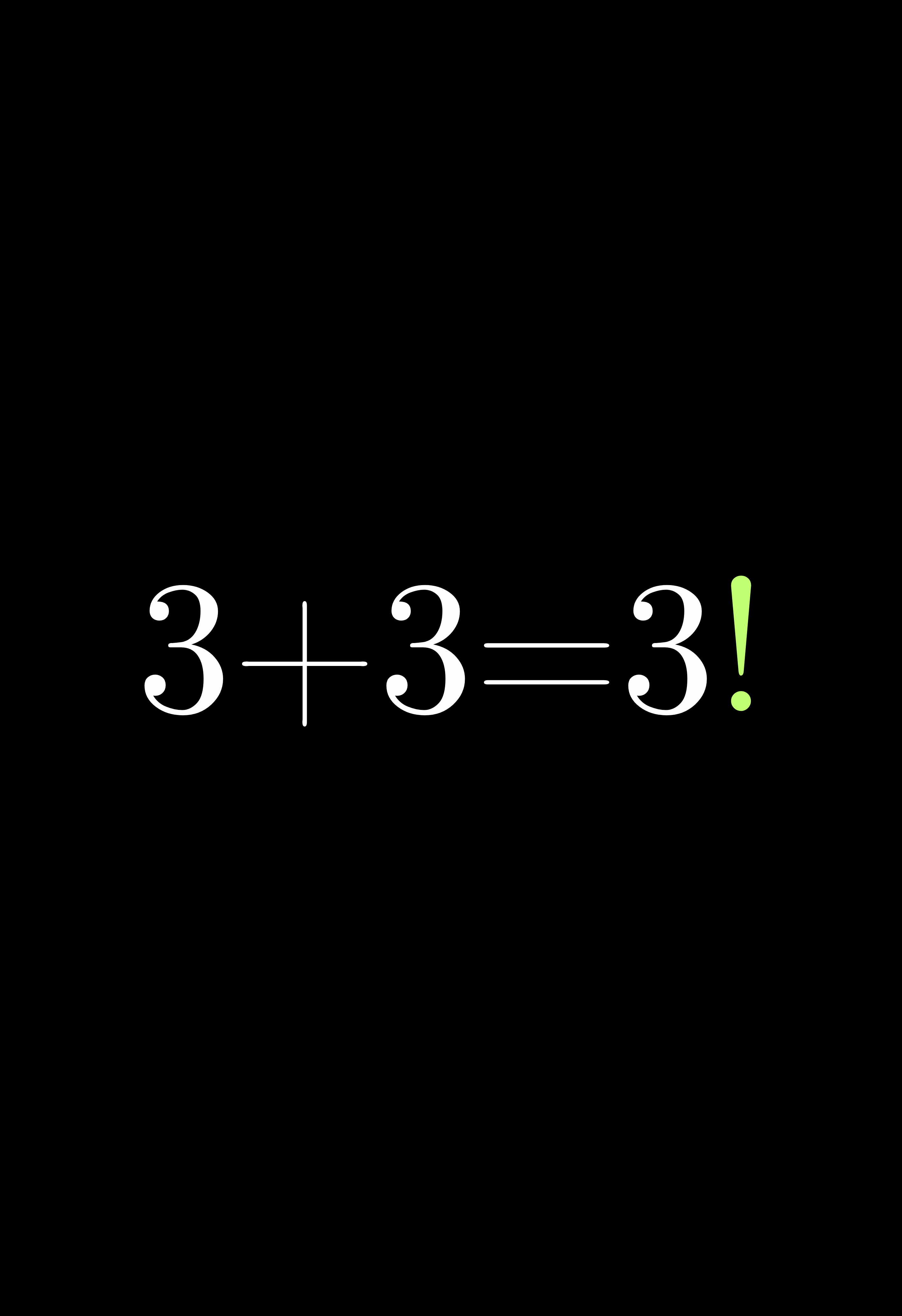


Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
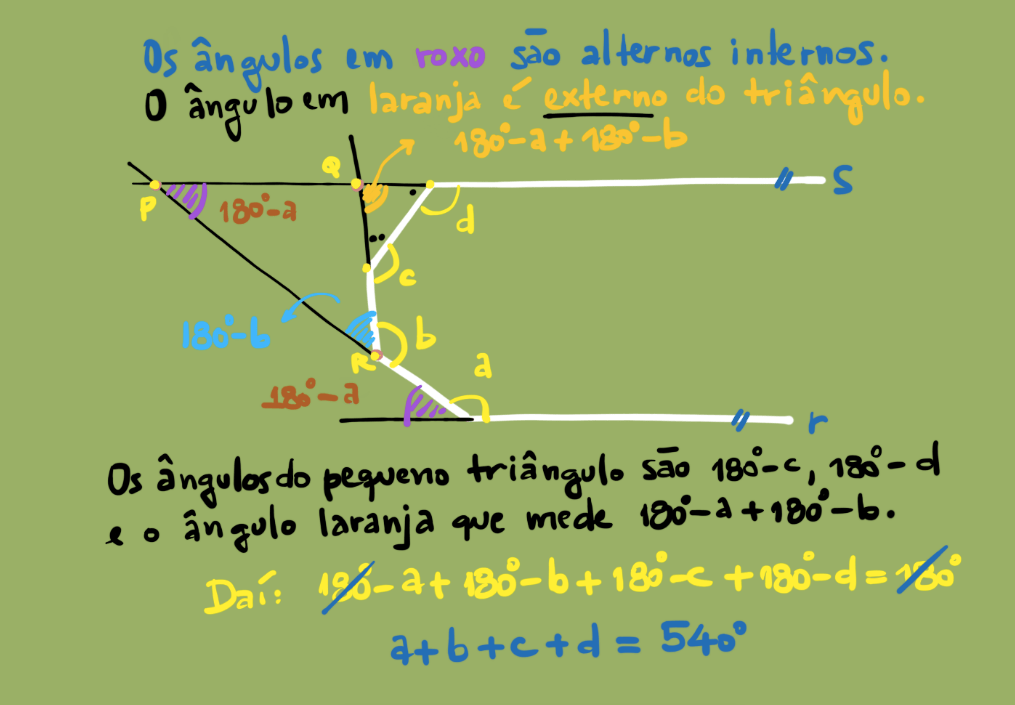
Segue a solução de mais uma dúvida de nossos alunos.
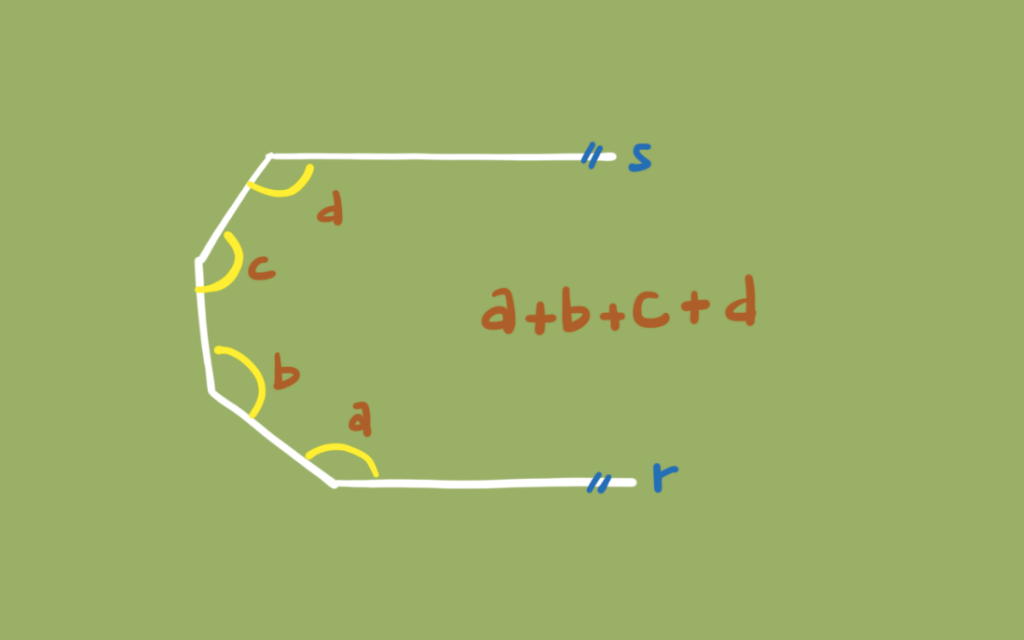
Segue abaixo a solução:
Siga nossas redes sociais:
@projeto.mentoria_
@equilateral_camisetas
Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Veja mais de nossos conteúdos:
Até a próxima!
[LSB]
Segue mais um problema enviado por um de nossos leitores:
Cuja solução segue abaixo:
É isso, até a próxima!
[LSB]
Entre em nossa loja de camisetas: http://reserva.ink/equilateral



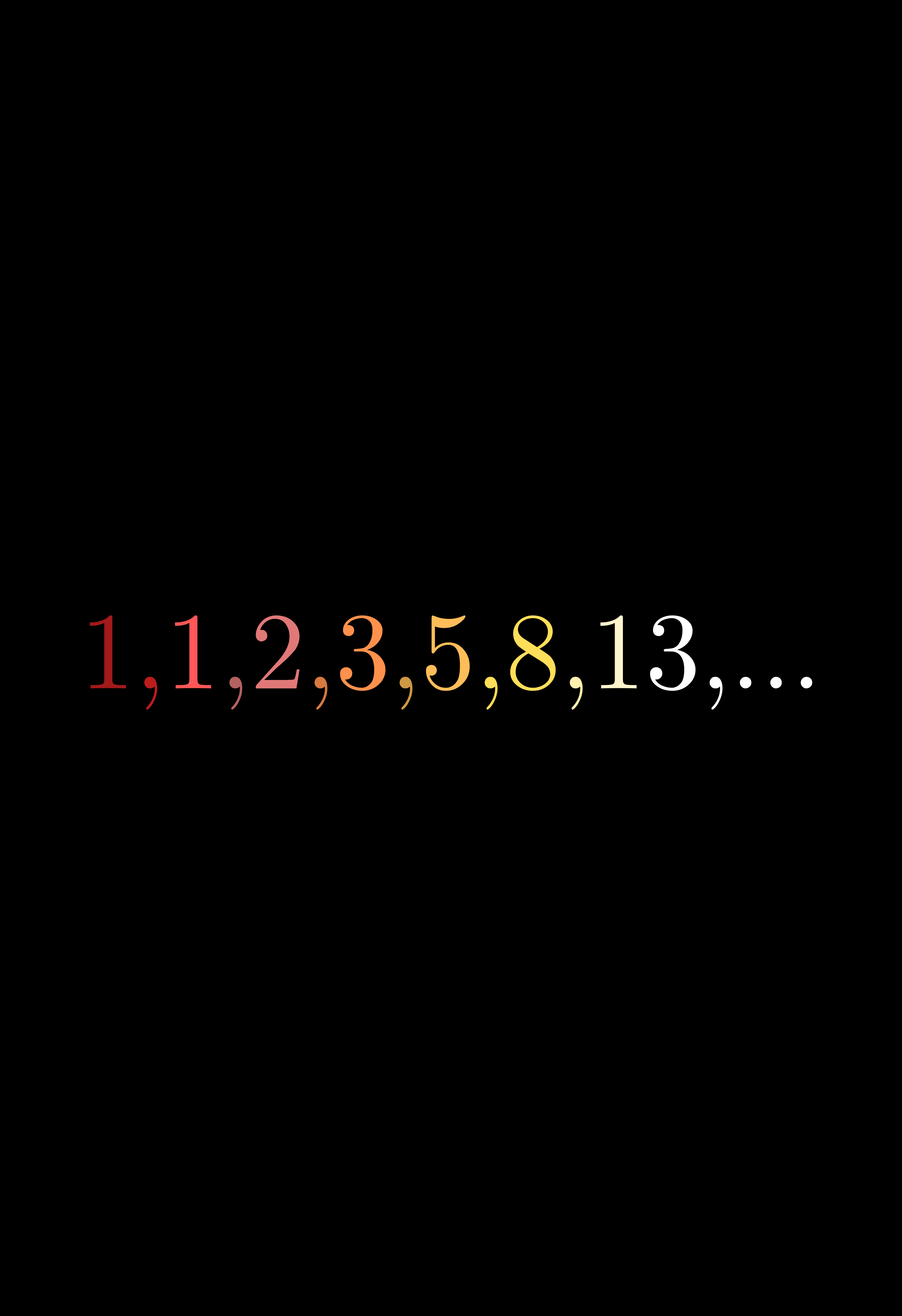
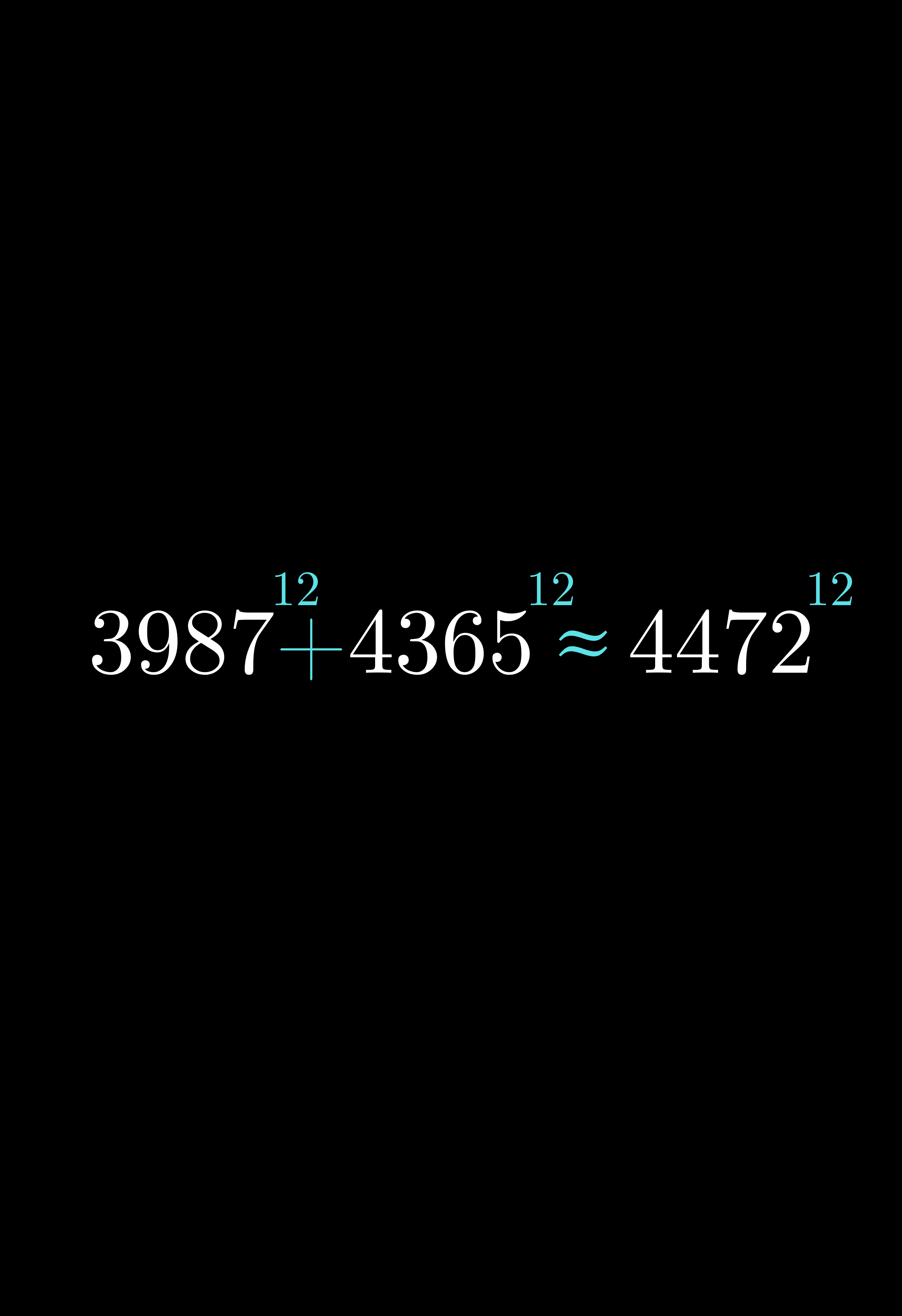





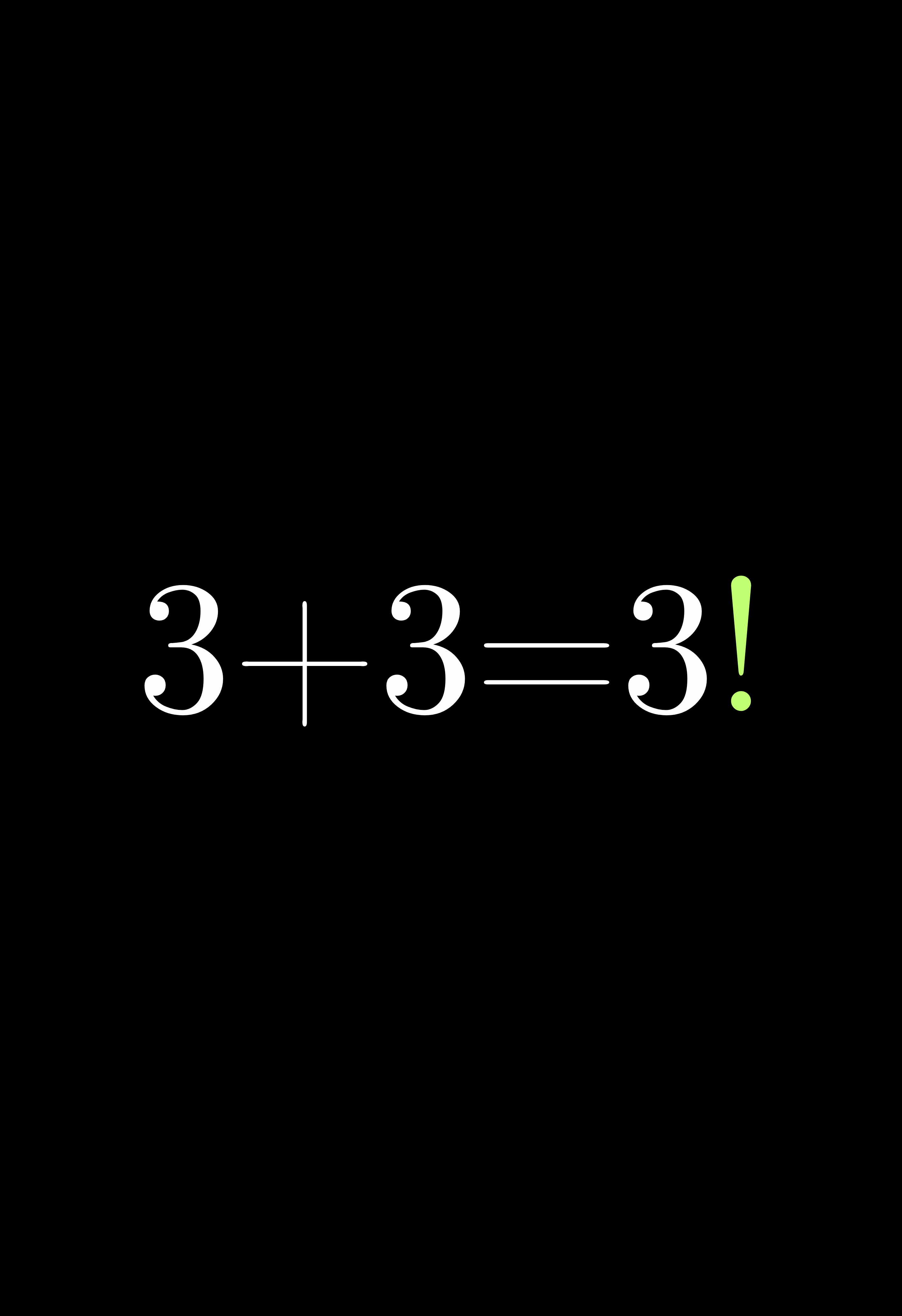
Com um pequeno atraso por questões alheias, publico o problema desta semana. Este exercício já é bem antigo, mas vale a pena conhecer, tanto pelo formato quanto pela ideia que ele traduz de o quão as equações são muito poderosas em resolver problemas elementares. Segue o enunciado:
Tenho o dobro da idade que você tinha quando eu tinha a idade que você tem. Quando você tiver minha idade, nossas idades somarão
. Quais serão nossas idades daqui a
anos?
Vale a pena a tentativa! Mãos a obra e bora pra cima!
Entre em nossa loja de camisetas: http://reserva.ink/equilateral
E compre camisetas como esta! Entrega em todo o Brasil!
[LSB]
Estamos de volta com o problema da semana. Vamos relembrar o enunciado antes de resolver. Segue:
Sendo
, calcular o valor de
.
Vamos à solução proposta pelo grande mentor e mestre Paulo de Sousa Sobrinho. Sabemos que:
Daí, elevando ambos os membros ao quadrado, teremos:
O que nos leva a:
Sabemos que e como
, podemos fazer
e teremos:
Esta é a solução proposta por nosso grande mestre Jaiminho.. ops, Paulinho! Vou propor uma nova solução em vídeo, um pouco menos elegante e, talvez…, um pouquinho mais longa, porém menos sofisticada.
Menção honrosa:
Listagem de problemas resolvidos até agora:
Até a próxima questão.
[LSB]
Veja nosso site de camisetas: http://reserva.ink/equilateral
Vamos a mais um problema da semana, desta vez proposto pelo ilustríssimo mentor Paulo de Sousa Sobrinho, mais conhecido por Paulinho. Segue o enunciado:
Sendo
, calcular o valor de
.
Agora é com você , mãos a obra e nos vemos em breve, na próxima solução.
Até lá.
[LSB]