Segue mais uma dúvida de nossos alunos:
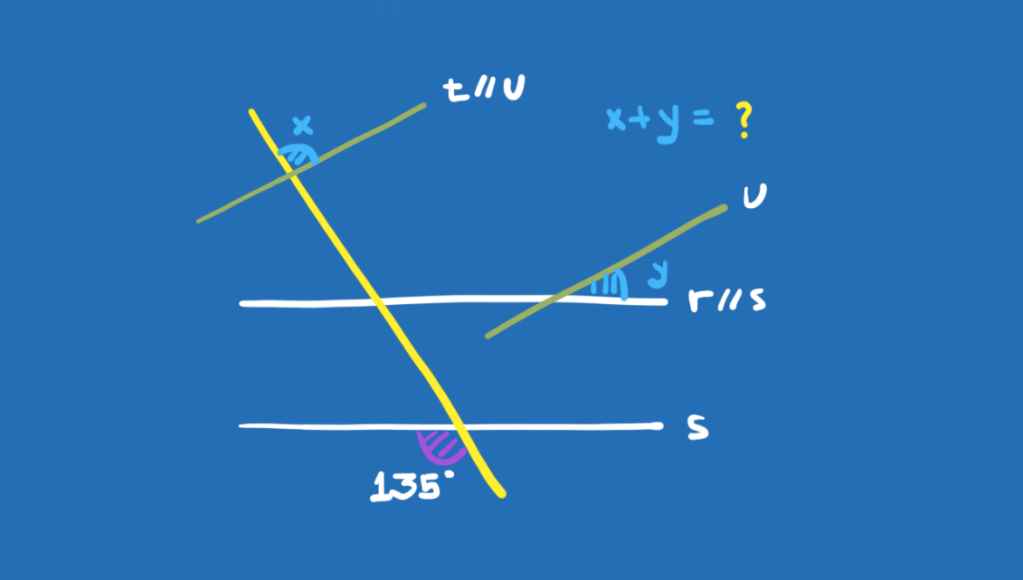
Cuja solução segue abaixo:
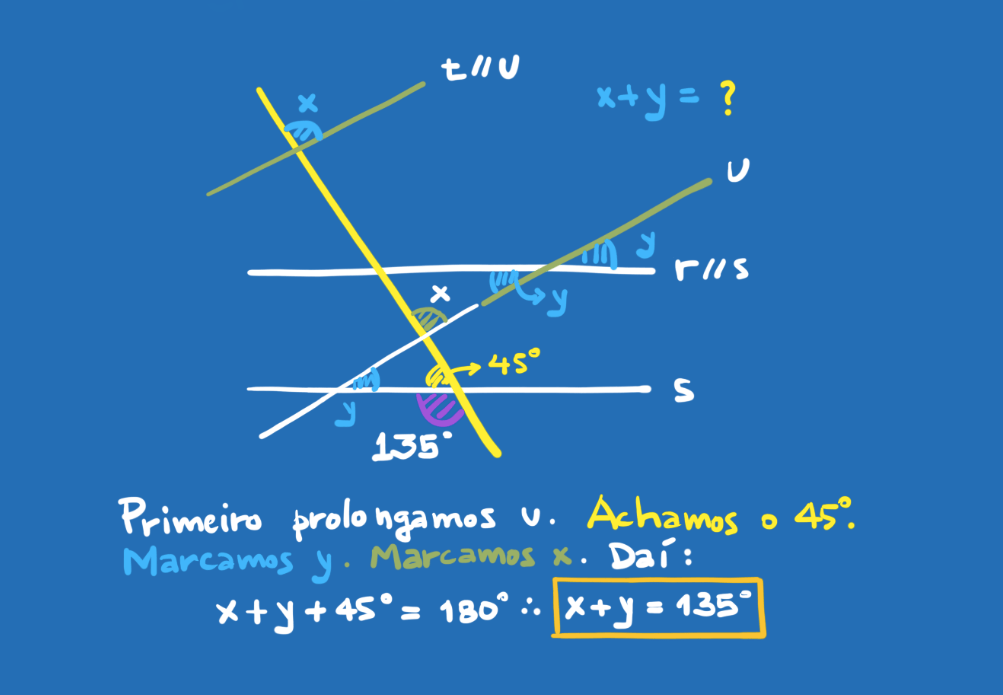
Nossa loja de camisetas: http://reserva.ink/equilateral
Segue mais uma dúvida de nossos alunos:
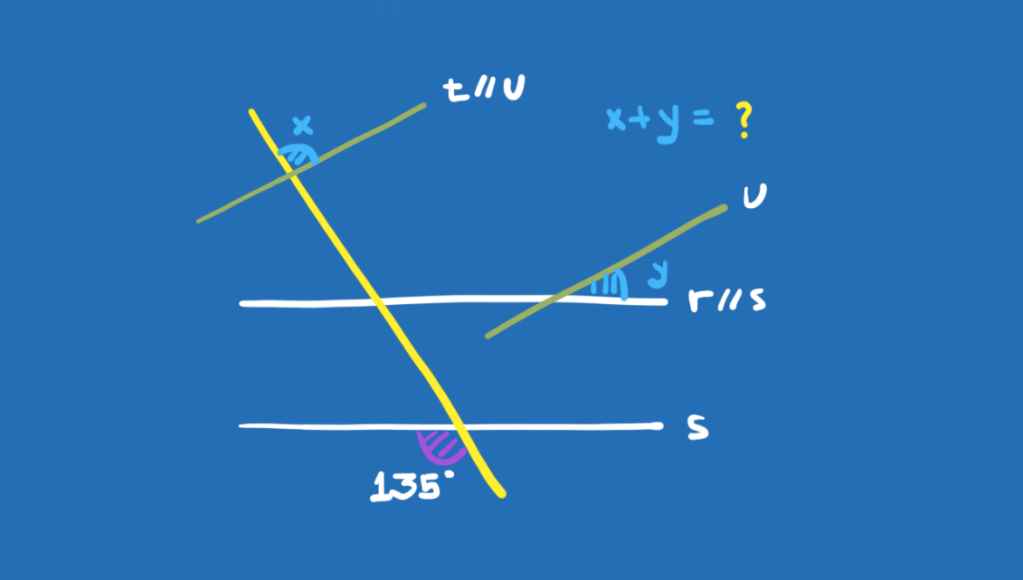
Cuja solução segue abaixo:
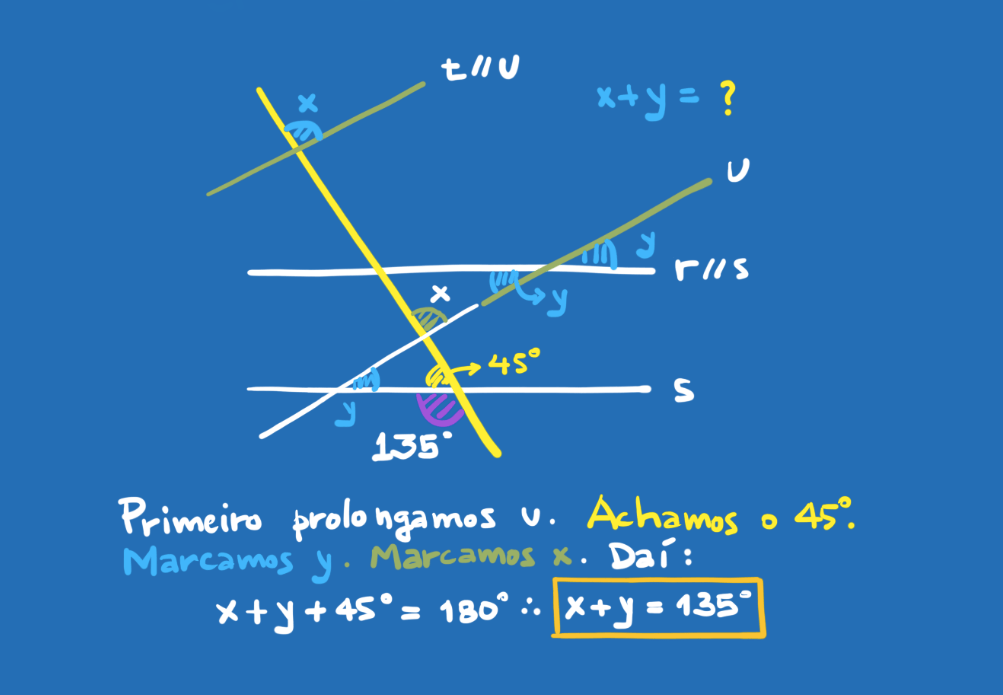
Nossa loja de camisetas: http://reserva.ink/equilateral
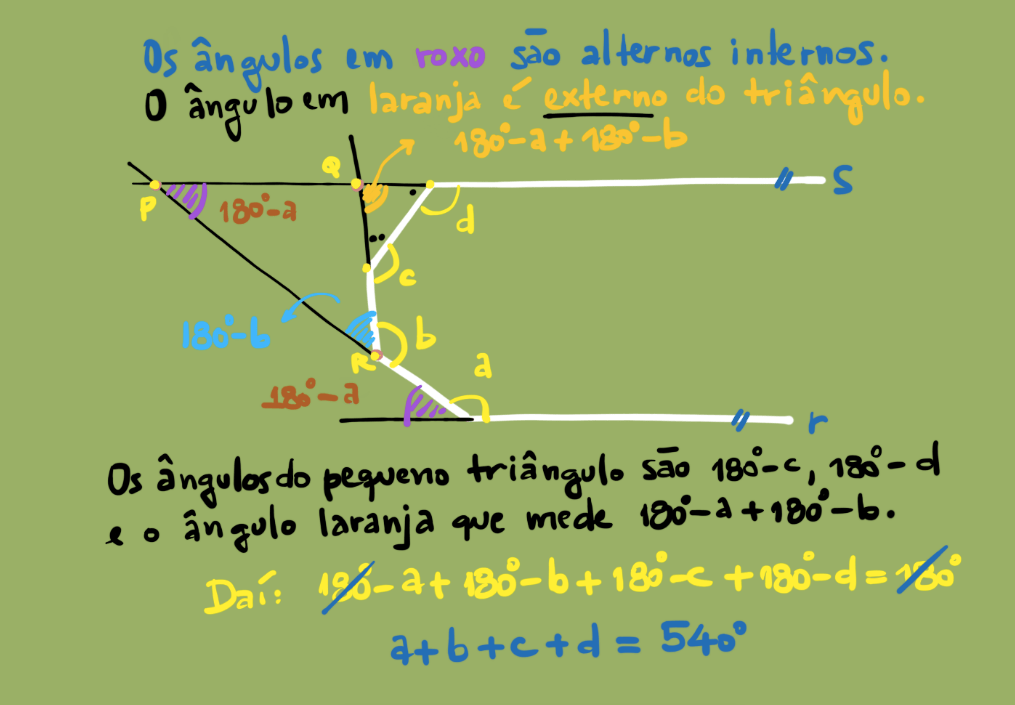
Segue um problema de geometria plana; simples, mas interessante.
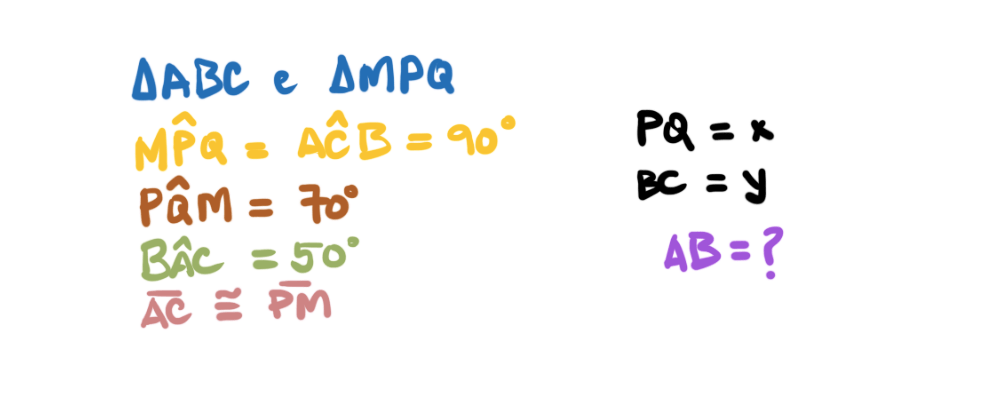
Quesemos encontrar o valor de . A solução segue abaixo:
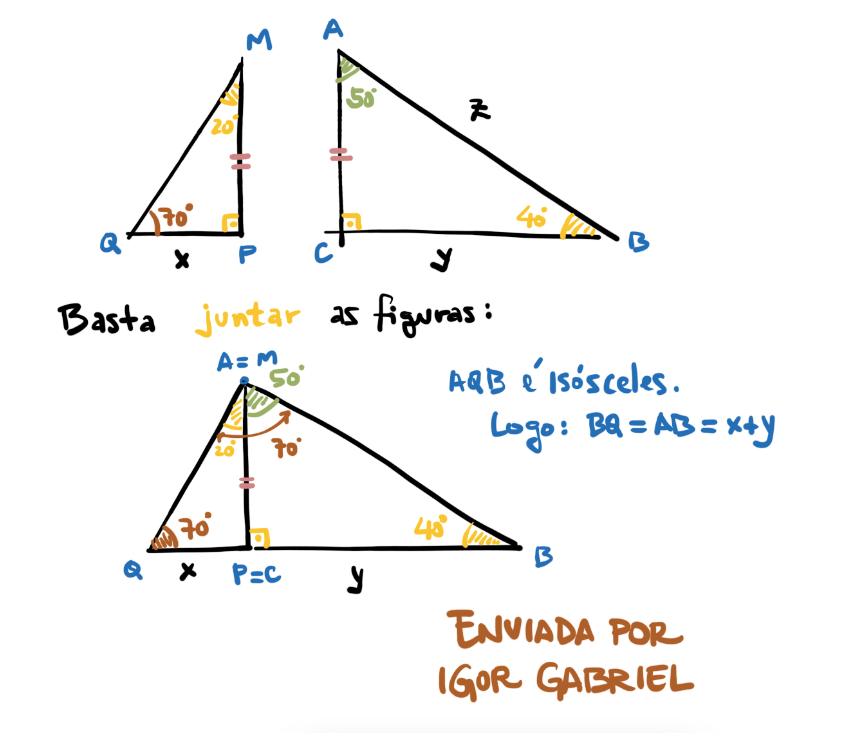
Até a próxima dúvida e boa semana!






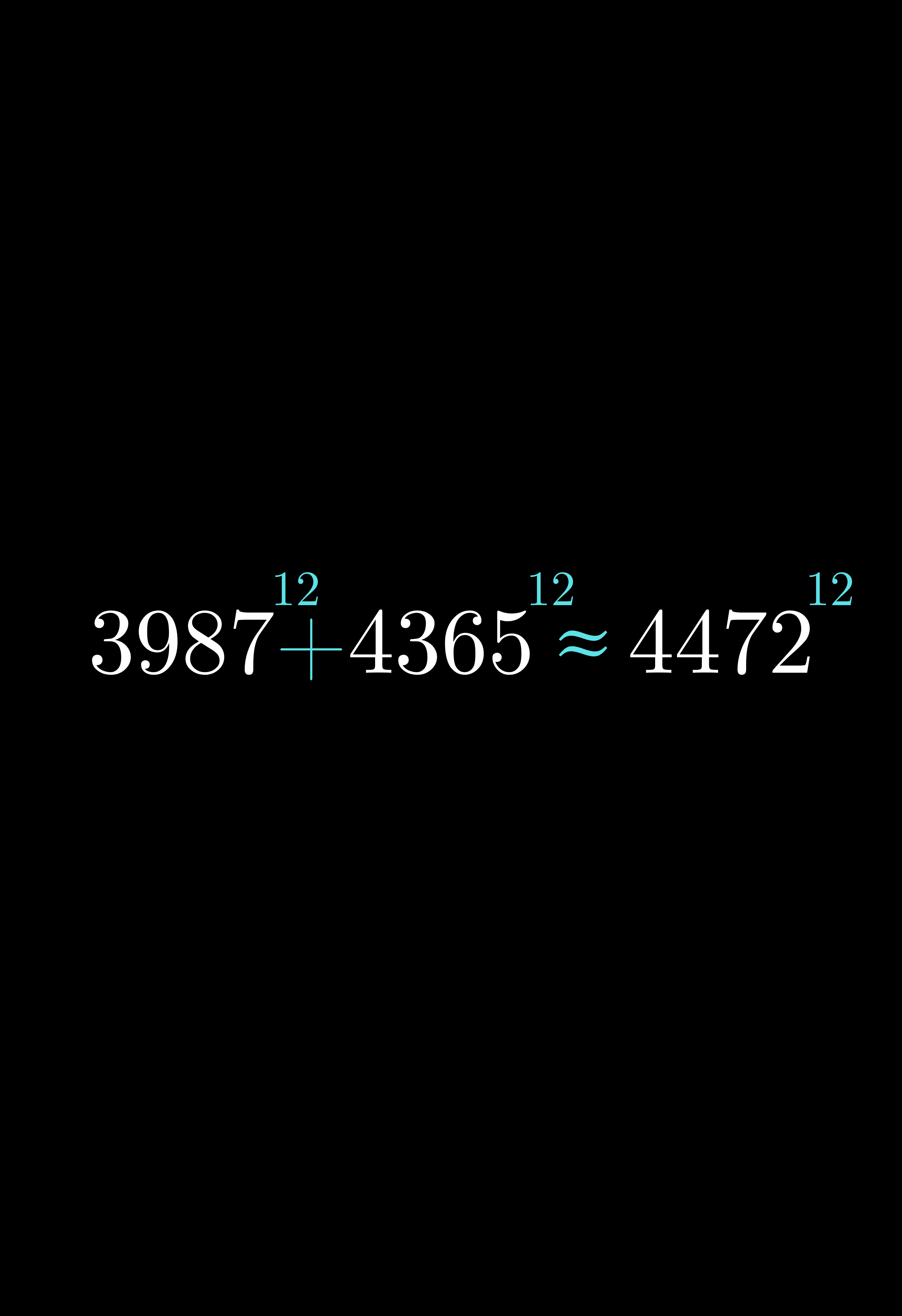






Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
Segue a solução de mais uma dúvida de nossos alunos.
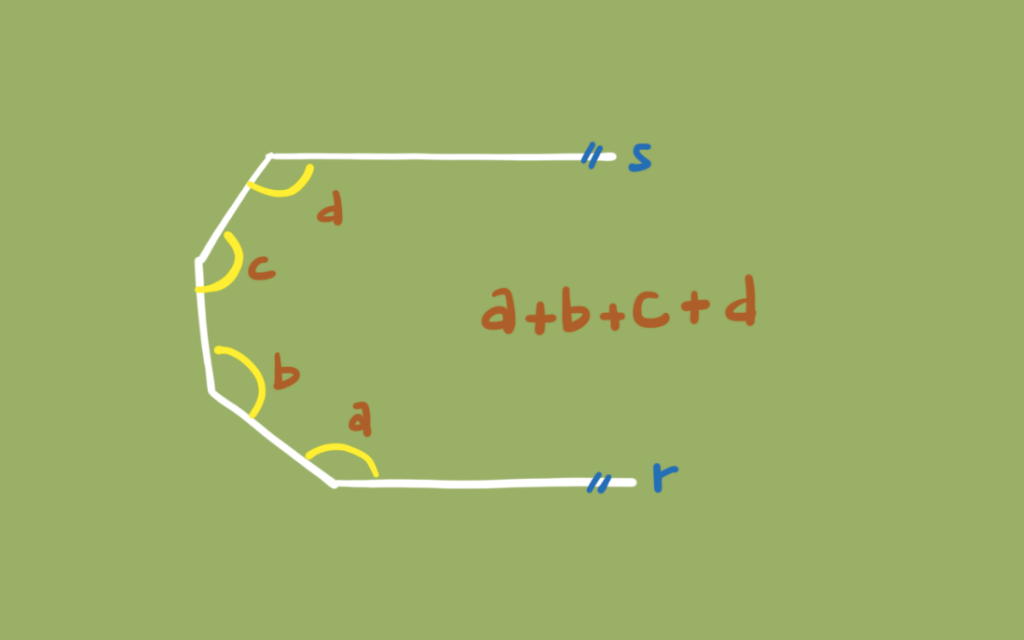
Segue abaixo a solução:
Siga nossas redes sociais:
@projeto.mentoria_
@equilateral_camisetas
Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Veja mais de nossos conteúdos:
Até a próxima!
[LSB]
Olá caros amigos, estamos de volta com mais uma LIVE aqui do canal do Youtube e, desta vez, trago até vocês um breve resumo de geometria plana.
Vamos aos trabalhos normais envolvendo estas publicações:
A imagem abaixo tem as questões resolvidas:
Eu sou Leonardo e você veio ao lugar certo pra aprender!
Está é uma iniciativa para trazer materiais de boa
qualidade até você e te ajudar a aprender mais.
Vamos crescer mais! Faça parte:
— Doe via PIX: leonardosantos.inf@gmail.com
— Siga-nos nas redes:
Instagram: http://www.instagram.com/mentorblog_oficial
Facebook: https://www.facebook.com/cursomentor
— DIVULGUE esta iniciativa!
Até a próxima!
[LSB]
Quer treinar um pouco os conceitos básicos de Geometria Plana e algumas propriedades de matrizes e de suas operações?
Então dá uma boa olhada nesse vídeo!
Você pode pegar as questões usadas neste material clicando AQUI.
Entre em nosso grupo no WhatsApp e receba semanalmente estas listas. Que são sempre corrigidas nas lives às quartas-feiras. Para entrar no grupo, clica AQUI.
A imagem com todas as questões resolvidas na live está logo abaixo.

Minha iniciativa é GRATUITA.
AJUDE:
👉🏼 Doe qualquer quantia via PIX: leonardosantos.inf@gmail.com
👉🏼 Siga-nos:
http://www.instagram.com/mentorblog_oficial
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800:
👉🏼 DIVULGUE esta iniciativa!
Até!
[LSB]
A lista de exercícios usada na live está disponível AQUI.
Você pode receber as listas semanalmente entrando em nosso grupo no WhatsApp, clicando AQUI.
As questões resolvidas estão na imagem abaixo:
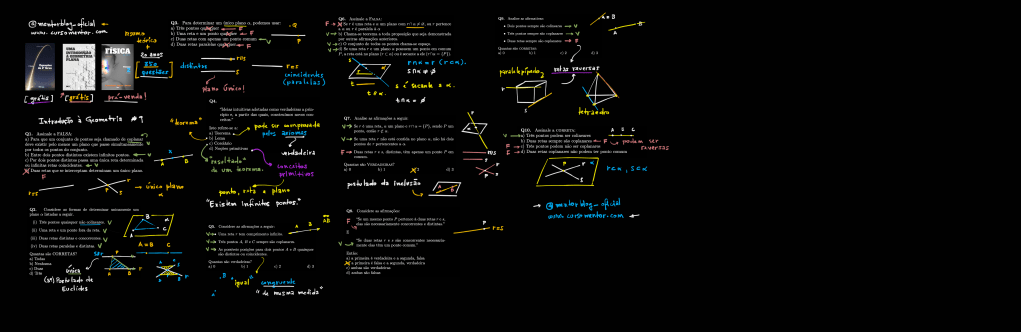
Minha iniciativa é GRATUITA.
AJUDE:
👉🏼 Doe qualquer quantia via PIX: leonardosantos.inf@gmail.com
👉🏼 Siga-nos:
http://www.instagram.com/mentorblog_oficial
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800:
👉🏼 DIVULGUE esta iniciativa!
Até!
[LSB]
Já tinha visto este problema? Só pra você saber ele já caiu na EsPCEx… fica ligado!
Minha iniciativa é GRATUITA.
AJUDE:
👉🏼 Doe qualquer quantia via PIX: leonardosantos.inf@gmail.com
👉🏼 Siga-nos:
http://www.instagram.com/mentorblog_oficial
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800:
👉🏼 DIVULGUE esta iniciativa!
Até!
[LSB]
Olá leitor.
Recebi um problema que envolve retas paralelas, semelhança e áreas em uma só questão. Vamos lá:
Na figura, os ângulos
,
,
são retos. Se
m e
m, a razão entre as áreas dos triângulos
e
é
a)
b)
c)
d)
e)
Vamos então à solução. Vamos chamar o ângulo . Assim teremos
. Como
, teremos
e, portanto os triângulos
e
são semelhantes. Assim, podemos escrever a relação:
Fazendo as áreas e calculando a razão entre elas:
Chegamos à opção B.
Até a próxima!
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]