Olá leitor,
a prova da Escola Naval de 2020/2021 trouxe uma questão que envolve o M.D.C de dois números e uma pergunta sobre probabilidade. Segue a questão:
(EN) Escolhendo aleatoriamente um número do conjunto  , qual a probabilidade de que o número escolhido e
, qual a probabilidade de que o número escolhido e  sejam primos entre si?
sejam primos entre si?
a) 
b) 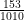
c) 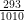
d) 
e) 
Enviada por Stephanie Wenceslau
Bom, primeiro, precisamos saber o que são números primos entre si ou ainda mutuamente primos. Dizemos que dois números naturais  e
e  são primos entre si, se
são primos entre si, se 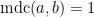 . O m.d.c. entre dois números naturais vale
. O m.d.c. entre dois números naturais vale 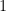 se eles não possuem fatores comuns em sua fatoração em primos. Por exemplo,
se eles não possuem fatores comuns em sua fatoração em primos. Por exemplo,  e
e  são primos entre si, pois veja que
são primos entre si, pois veja que 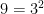 e
e  .
.
É possível ver que dois números pares nunca são primos entre si, pois ambos são divisíveis por  ; e, que dois números primos também sempre são primos entre si, por conta da própria definição de números naturais primos.
; e, que dois números primos também sempre são primos entre si, por conta da própria definição de números naturais primos.
Assim, fatorando  , encontramos
, encontramos 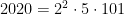 . Ou seja, todos os múltiplos de
. Ou seja, todos os múltiplos de  ,
,  ou
ou 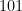 não serão primos com
não serão primos com  , pois haverá fatores comuns em suas fatorações, tornando o m.d.c entre eles maior que
, pois haverá fatores comuns em suas fatorações, tornando o m.d.c entre eles maior que 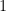 .
.
Vamos contar então, primeiramente, os múltiplos de  . Eles são em número
. Eles são em número  . Para
. Para  , temos
, temos  . Finalmente, para
. Finalmente, para 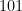 , ficamos com
, ficamos com 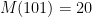 .
.
Agora, ao somarmos estes valores, teremos  . Porém, precisamos atentar para o fato de que, estamos contando números repetidos, uma vez que os múltiplos de
. Porém, precisamos atentar para o fato de que, estamos contando números repetidos, uma vez que os múltiplos de 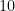 , por exemplo, são múltiplos de
, por exemplo, são múltiplos de  e de
e de  também; sendo, portanto, recontados. Vamos excluí-los.
também; sendo, portanto, recontados. Vamos excluí-los.
Os múltiplos de  e de
e de  são os múltiplos de
são os múltiplos de 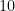 , e são
, e são  . Para os múltiplos de
. Para os múltiplos de  e de
e de 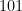 , teremos
, teremos  ; e, finalmente, os múltiplos de
; e, finalmente, os múltiplos de  e de
e de 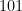 são em número total de
são em número total de  . Estes serão excluídos. O total é
. Estes serão excluídos. O total é 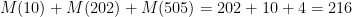 .
.
Ainda precisamos considerar os múltiplos simultâneos de  ,
,  e
e 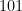 , que serão os múltiplos de
, que serão os múltiplos de  . Estes são excluídos mais de uma vez e precisam ser reincluídos. Então
. Estes são excluídos mais de uma vez e precisam ser reincluídos. Então 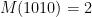 .
.
Finalmente podemos encontrar todos os números naturais que têm fatores comuns com  , não sendo primos com
, não sendo primos com  . Assim, eles são
. Assim, eles são  no total. Como são
no total. Como são  números no total, temos
números no total, temos 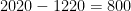 números que são primos entre si com
números que são primos entre si com  . Agora, temos a probabilidade:
. Agora, temos a probabilidade:

Opção A.
E aí, gostou.
Siga-me e ajude divulgando.
Minha iniciativa é GRATUITA.
Você pode AJUDAR:
— Doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
— Pelo APOIA SE:
https://apoia.se/mentor
— Nos seguindo:
http://www.instagram.com/curso_mentor_oficial
Mas, claro, fique a vontade, qualquer ajuda é bem vinda!
E a melhor ajuda que você pode dar é GRÁTIS, DE GRAÇA, 0800: só basta DIVULGAR esta iniciativa!
Entre em nosso canal no Telegram: https://t.me/cursomentor
Apoiadores:
Edson Pereira Barros
Até!
[LSB]