Tira-Teima #2

Problema da Semana #10: Uma Solução Mais ou Menos Simples

Segue a solução do problema da semana #10. Vamos relembrar o enunciado.

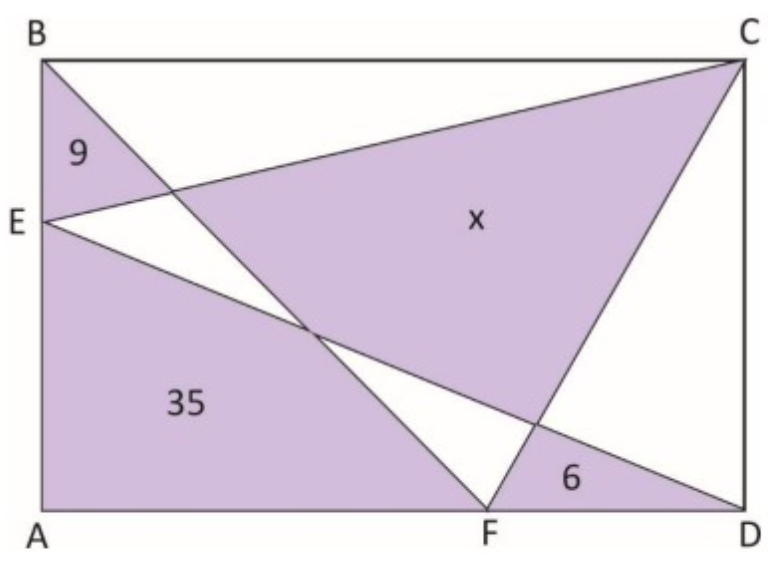
Na figura abaixo, o terreno retangular $ABCD$ foi loteado e os números que aparecem no interior de alguns destes lotes, indicam suas respectivas áreas em $\text{km}^2$ .

A medida da área indicada pelo lote da letra $x$ , em $\text{km}^2$ é igual a:

a) $70$

b) $40$

c) $60$

d) $50$

e) $54$

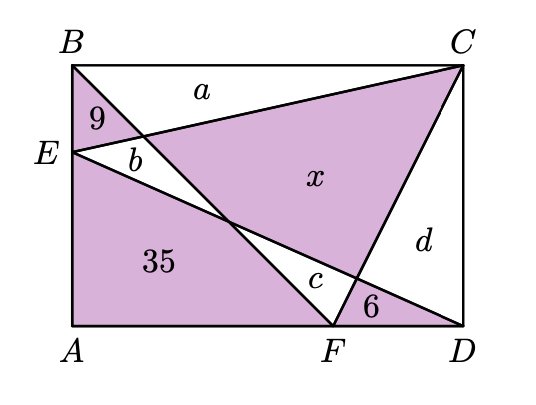
Uma solução “simples” é chamar a áreas desconhecidas em branco de $a$ , $b$ , $c$ e $d$ . Como na figura abaixo:

Perceba que a área do triângulo $BCF$ é igual à área do triângulo $CDE$ , pois ambos são iguais a metade da área do retângulo (esse pode ser um fato difícil de perceber, pense um pouco até que isso fique claro para você). Assim, podemos escrever:

$a+x + c = b + x + d \Leftrightarrow a+c = b+d$

Pelo mesmo motivo teremos:

$9 + b + 35 + 6 + d = a + x + c \Leftrightarrow 50 + \underbrace{b + d}_{= a+c} = x + a + c$

Logo $x = 50$ . Há outra solução usando o Teorema dos Carpetes. Mas essa deixaremos para o grande mentor José Maria Gomes (o famoso China).

Resolveram este Problema:

Micael França

Listagem de problemas resolvidos até agora:

(3) Ygor Gabriel
(3) Micael França
(2) Yasmim Silva
(2) Ygor Farias
(2) Arthur Rocha
(2) @mariopersico_
(2) Iuri Henrique
(1) Alef
(1) Lucca Gabriel
(1) Gustavo
(1) Lucas Lopes
(1) Davi do Nascimento Teles Barata
(1) Enzo Botarelli

Se seu nome não apareceu, me avise pois pode ser que eu não tenha visto a sua solução enviada.

Bora pra cima!

Um Problema do ITA: Cinemática Escalar

Existem muitos problemas de cinemática elementar que são muito difíceis. Especialmente quando os cronômetros de dois objetos não estão sincronizados, fazendo com que seus instantes iniciais de contagem de tempo sejam diferentes.

Trazemos então o seguinte problema, do ITA, um vestibular extremamente difícil que exige um alto nível de conhecimento de seus candidatos nas áreas de Matemática, Física, Química, Língua Portuguesa e Lingua Inglesa. Segue o enunciado do problema:

Um móvel $A$ parte da origem $O$ , com velocidade inicial nula, no instante $t_0 = 0$ e percorre o eixo $Ox$ com aceleração constante $a$ . Após um intervalo de tempo $\Delta t$ , contado a partir da saída de $A$ , um segundo móvel $B$ parte de $O$ com uma aceleração igual a $n \cdot a$ , sendo $n > 1$ . $B$ alcançará $A$ no instante:

a) $t = \left(\frac{\sqrt{n}}{\sqrt{n} - 1} + 1\right)\Delta t$

b) $t = \left(\frac{\sqrt{n}}{\sqrt{n} - 1} - 1\right)\Delta t$

c) $t = \left(\frac{\sqrt{n}-1}{\sqrt{n}}\right)\Delta t$

d) $t = \left(\frac{\sqrt{n}+1}{\sqrt{n}}\right)\Delta t$

e) $t = \left(\frac{\sqrt{n}}{\sqrt{n}-1}\right)\Delta t$

O móvel $A$ move-se a partir do repouso com aceleração $a$ , o que ocorre durante um $\Delta t$ , ou seja, seus espaços em função do tempo ficam dados pela equação:

$S_A = S_{0_A} + v_{0_A} \Delta t_A + \frac{a}{2} (\Delta t_A)^2$

Para o móvel $B$ teremos:

$S_B = S_{0_B} + v_{0_B} (\Delta t_B) + \frac{n \cdot a}{2} (\Delta t_B)^2$

Sabemos que o móvel $A$ partiu do repouso, portanto $v_{0_A} = 0$ e queremos saber em que instantes $A$ e $B$ se encontrarão, ou seja, quando teremos $S_A = S_B$ , assim:

$S_A = S_B \Leftrightarrow S_{0_A} + \frac{a}{2} (\Delta t_A)^2 = S_{0_B} + v_{0_B} (\Delta t_B) + \frac{n \cdot a}{2} (\Delta t_B)^2$

Como $A$ e $B$ partem do mesmo ponto temos $S_{0_A} = S_{0_B}$ e, então:

$\frac{a}{2} (\Delta t_A)^2 = v_{0_B} (\Delta t_B) + \frac{n \cdot a}{2} (\Delta t_B)^2$

Agora faremos uma suposição crucial: a de que $v_{0_B} = 0$ , admitindo que $B$ também partiu do repouso, daí:

$\frac{a}{2} (\Delta t_A)^2 = \frac{n \cdot a}{2} (\Delta t_B)^2$

Então, como $n \cdot a \geq 0$ , teremos:

$\sqrt{\frac{a}{2}} \cdot \Delta t_A = \sqrt{\frac{n \cdot a}{2}} (\Delta t_B) \Leftrightarrow \sqrt{\frac{a}{2}} \cdot \Delta t_A = \sqrt{n} \cdot \sqrt{\frac{a}{2}} (\Delta t_B)$

Simplificando $\sqrt{\frac{a}{2}}$ em ambos os membros teremos:

$\Delta t_A = \sqrt{n} \cdot (\Delta t_B)$

Chegamos onde queríamos. Veja que $\Delta t_A = t - t_{0_A}$ e que $t_{0_A} = 0$ , ou seja, $\Delta t_A = t$ . Por outro lado, $\Delta t_B = t - t_{0_B}$ e $t_{0_B} = \Delta t$ , portanto $\Delta t_B = t - \Delta t$ ; assim:

$t = \sqrt{n} (t - \Delta t) \Leftrightarrow t = \sqrt{n} \cdot t - \sqrt{n} \cdot \Delta t$

Finalmente, podemos escrever: $\sqrt{n} \cdot t - t = \sqrt{n} \Delta t$ . Ou como aparece nas opções:

$t = \left(\frac{\sqrt{n}}{\sqrt{n} - 1}\right) \Delta t$

Opção E.

O problema foi enviado por Arthur Rocha.

Até a próxima.

[LSB]

ITA: uma Questão de Combinatória!

Olá leitor!

Segue uma questão sobre análise combinatória trazida até mim.

(ITA) Uma escola possui $18$ professores, sendo $7$ de Matemática, $3$ de Física e $4$ de Química. De quantas maneiras podemos formar comissões de $12$ professores de modo que cada uma contenha exatamente $5$ professores de Matemática, no mínimo $2$ de Física e no máximo $4$ de Química?
a) $875$
b) $1877$
c) $1995$
d) $2877$
e) N.D.A.
Enviada por Caio Franco

Esse é o tipo de problema que a boa e velha tática de separar em casos ajuda bastante. Vamos montar uma tabela com as possibilidades de números de professores, sendo $M$ para Matemática; $F$ para Física; $Q$ para Química e $O$ para as outras disciplinas.

$\begin{array}{c | c | c | c} M & F & Q & O \\ \hline 5 & 3 & 0 & 4 \\ 5 & 3 & 1 & 3 \\ 5 & 3 & 2 & 2 \\ 5 & 2 & 1 & 4 \\ 5 & 2 & 2 & 3 \\ \end{array}$

Assim, o total de escolhas será:

${7 \choose 5} \cdot {3 \choose 3} \cdot {4 \choose 0} \cdot {4 \choose 4} + {7 \choose 5} \cdot {3 \choose 3} \cdot {4 \choose 1} \cdot {4 \choose 3} + {7 \choose 5} \cdot {3 \choose 3} \cdot {4 \choose 2} \cdot {4 \choose 2} + {7 \choose 5} \cdot {3 \choose 2} \cdot {4 \choose 1} \cdot {4 \choose 4} + {7 \choose 5} \cdot {3 \choose 2} \cdot {4 \choose 2} \cdot {4 \choose 3}$

Podemos colocar ${7 \choose 5}$ em evidência:

${7 \choose 5} \cdot (1 \cdot 1 \cdot 1 + 1 \cdot 4 \cdot 4 + 1 \cdot 6 \cdot 6 + 3 \cdot 4 \cdot 1 + 3 \cdot 6 \cdot 4) = \frac{7!}{5! \cdot 2!} \cdot (1 +16 + 36 + 12 + 72) = 21 \cdot 137 = 2877$