Segue um problema de geometria plana; simples, mas interessante.
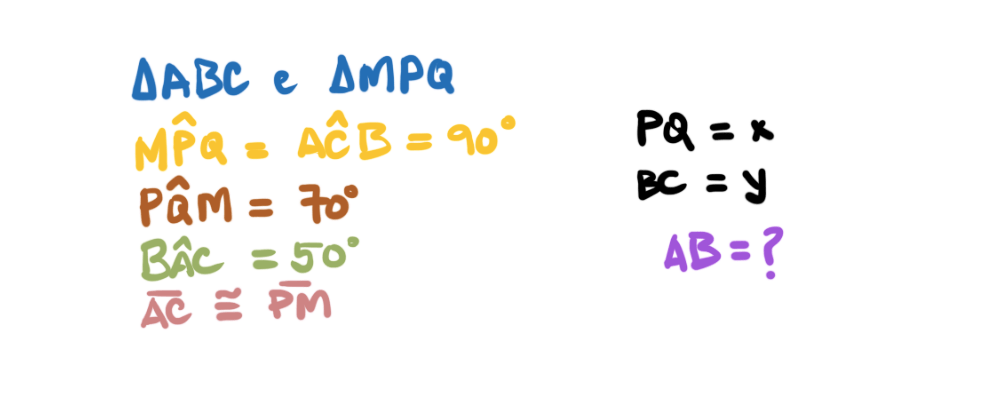
Quesemos encontrar o valor de . A solução segue abaixo:
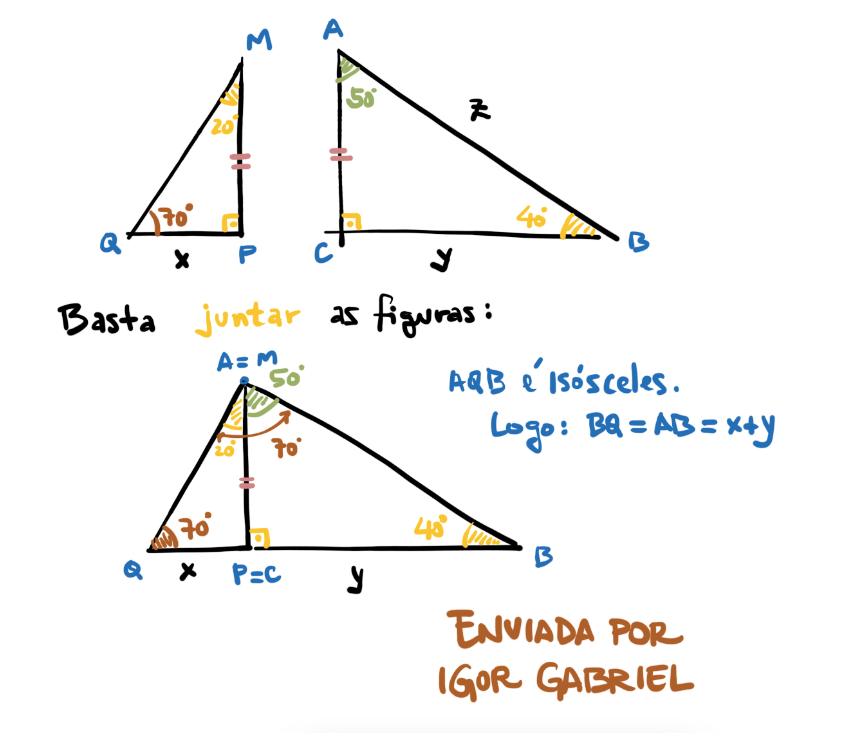
Até a próxima dúvida e boa semana!












Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
Segue um problema de geometria plana; simples, mas interessante.
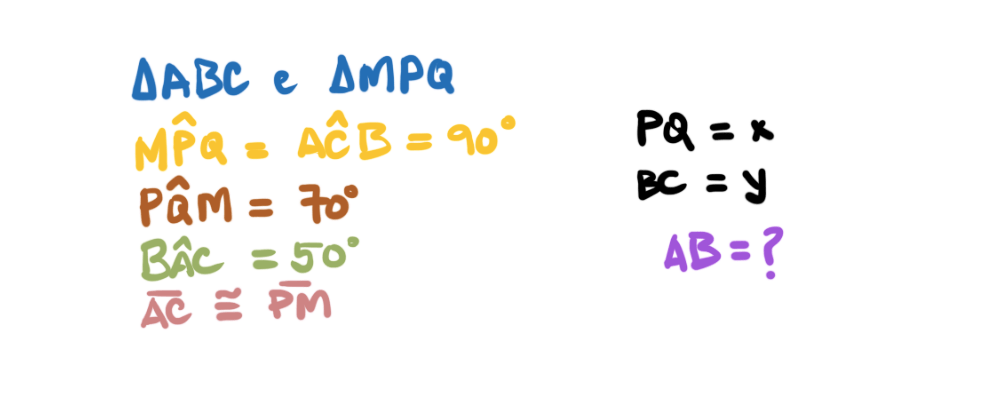
Quesemos encontrar o valor de . A solução segue abaixo:

Até a próxima dúvida e boa semana!













Compre em nossa loja de camisetas: www.reserva.ink/equilateral
Confira outros conteúdos:
Olá, nesta postagem queremos trazer um exemplo de problema que exige o conhecimento, mesmo que básico sobre os principais pontos notáveis do triângulo. Em particular, estamos falando sobre o incentro. Em vez de apenas resolver o problema, queremos falar um pouco sobre este ponto notável, aproveitando como uma revisão básica.
Por definição, o incentro é o ponto de encontro das bissetrizes internas de um triângulo. As bissetrizes internas de um triângulo são segmentos que tem um extremo sendo o vértice do triângulo e o outro vértice sobre o lado do triângulo, ou seja é uma ceviana.
Na figura anterior, no triângulo ,
,
e
são cevianas. Se tivermos
,
e
então as três cevianas serão bissetrizes internas.
Uma observação importante aqui: não estamos provando que as três bissetrizes internas concorrem (se interceptam) no mesmo ponto (isto ficará pra outro momento…), mas por ora, vamos admitir que seja verdade, já que, da fato, é.
Assim, feita esta breve observação e “dados nomes aos bois” chamaremos o ponto o de incentro do triângulo
. E, claro, pela própria construção da figura, é intuitivo que o incentro é sempre interno ao triângulo, seja ele acutângulo, retângulo ou obtusângulo.
Por uma questão de simplificação, vamos convencionar que ângulos de mesma cor têm a mesma medida. Sabendo que tangentes comuns traçadas de um mesmo ponto a uma circunferência são iguais, o incentro de um triângulo é o centro do círculo inscrito no mesmo triângulo.
Assim, na figura anterior, os ângulos em laranja são todos retos (valem ) e
, em que
é o raio do círculo inscrito, também chamado de incírculo. Fiz essa figura pra que seja percebido que os “pés” das bissetrizes não são, necessariamente, pontos do círculo inscrito.
Esta figura traz várias consequências implícitas. Por exemplo, os triângulos de mesma cor na figura a seguir, são congruentes. Mostrando, por exemplo que ,
e
.
Assim, veja que o incentro está a uma mesma distância de cada um dos lados do triângulo.
Com base nesta figura, só para citar uma propriedade importante, podemos mostrar que . Como não é nosso foco, fica pra depois. Bom qual nosso foco, no momento então? A relação entre o angulo interno do vértice
e o ângulo
na figura a seguir:
Veja que é o incentro, pois
e
são bissetrizes internas. Assim, teremos as seguintes relações:
para o triângulo
e também
Fica, então, simples de se perceber que:
Ou seja:
ou
Vamos então ao problema proposto na EEAr há algum tempo, que trago aqui com uma ligeira adaptação:
(EEAr — Modificada)
Um triângulo
tem
com incentro. Se
, qual o valor de
?
a)
b)
c)
d)
Veja que o problema trata exatamente do que acabamos de ver. Como é incentro, basta fazermos:
Assim:
Portanto, letra D.
Ah, e aqui está um vídeo sobre todos os pontos notáveis do triângulo.
Espero ter esclarecido um pouco mais sobre o incentro e suas propriedades.
Minha iniciativa é gratuita.
Você pode ajudar doando qualquer quantia via PIX: leonardosantos.inf@gmail.com
Fique a vontade, qualquer ajuda é bem vinda! E a melhor ajuda que você pode dar não custa nada: só basta divulgar esta iniciativa!
Até!
[LSB]
Olá leitores,
passou o carnaval e voltamos com força total. Estas foram as listas das últimas três semanas. Demoramos um pouco mais por conta de uma rotina bem apertada de trabalho fora do site. Mas estamos na linha novamente. E com muitas novidades.
Foi isso galera.
Bom fim de semana e bons estudos.
Olá,
estamos fechando mais uma semana (semana #6) na turma pré-AFA de 2019. Mas não é por isso que vamos deixar de publicar por aqui as listas da semana #5.
Esta foi uma semana produtiva para nós e esperamos que seja para vocês também.
Bons estudos e bom fim de semana.
[LSB]
Olá alunos, mais um vídeo. Nesta aula de geometria analítica falamos sobre a área de um triângulo qualquer no plano cartesiano e damos um exemplo de como utilizar o algoritmo que calcula esta área.
Seja Patrão! Tenha acesso a conteúdo exclusivo, inscrevendo-se em nosso PATREON:
http://www.patreon.com/mentor
Veja muitos exercícios (com gabarito) sobre este assunto em:
https://cursomentor.com/downloads/listas-de-exercicios/matematica/
Veja também muitos exercícios de outros assuntos indo em: http://www.cursomentor.com
Curta nossa fanpage: http://www.facebook.com/cursomentor
Siga-nos no Twitter:
http://www.twitter.com/curso_mentor
Bons estudos e sucesso.
Olá alunos e assinantes, estamos de volta para uma de nossas aulas e, neste vídeo, abordamos a fórmula que determina as coordenadas do baricentro de um triângulo no plano cartesiano. Não fazemos uma demonstração, mas mostramos como é damos um exemplo de utilização.
Seja Patrão! Tenha acesso a conteúdo exclusivo, inscrevendo-se em nosso PATREON:
http://www.patreon.com/mentor
Veja muitos exercícios (com gabarito) sobre este assunto em:
https://cursomentor.com/downloads/listas-de-exercicios/matematica/
Veja também muitos exercícios de outros assuntos indo em: http://www.cursomentor.com
Curta nossa fanpage: http://www.facebook.com/cursomentor
Siga-nos no Twitter:
http://www.twitter.com/curso_mentor
Bons estudos e sucesso.
Olá leitores,
estamos publicando freneticamente no nosso canal do YouTube (wwww.youtube.com/c/cursomentor) e por isso temos publicado um pouco menos por aqui, mas isto não quer dizer que não tenhamos colocado novas listas de exercícios. Confira estas quatro novas listas que estão em nossa página de exercícios já há alguns dias.
Um abraço e bons estudos.
@LSBar – CEO & Founder
Questão enviada por Ederson Ferreira
(CONED-CASTANHAL 2009-PA) De um ponto qualquer marcado no interior de um triângulo equilátero traçam-se segmentos perpendiculares a todos os lados. Podemos afirmar que a soma dos comprimentos dos segmentos traçados é igual a:
a) Medida do lado do triângulo
b) Medida da altura do triângulo
c) Medida da metade do lado do triângulo
d) Medida da metade da altura do triângulo
e) Medida da área do triângulo
Veja a solução aqui.